Teste de Diversificação com Ações da B3

Diversificar, de fato, diminui o risco de um portfólio?

A ideia de teste aqui é simples. Será que ao utilizar dados reais da bolsa brasileira, conseguirmos demonstrar que, de fato, há ganhos de diversificação?

Como de costume, vamos checar quais são os pacotes necessários para o script. Faremos uso de cinco, sendo esses: a) BatchGetSymbols; b) tidyverse; c) highcharter; d) pracma; e) reshape2.

O primeiro pacote, BatchGetSymbols, é útil com duas funções que utilizaremos na captura de dados reais. A primeira função, GetIbovStocks(), nos ajuda a obter a lista de ações (por ticker) que atualmente fazem parte da carteira teórica do Índice Ibovespa e estão disponíveis na lista do site da B3. Maiores detalhes da lista em: http://www.bmfbovespa.com.br/pt_br/produtos/indices/indices-amplos/indice-ibovespa-ibovespa-composicao-da-carteira.htm. A segunda função do pacote é a BatchGetSymbols(). Através dessa função, podemos apresentar a lista de tickers, a data de início e a data final para fazer o download das séries históricas contidas na base do Yahoo Finance.

O segundo pacote nos é util para manipular base de dados no formato dataframe. Obteremos os dados através da BatchGetSymbols(). Todavia, esses vem em um formato de list e os valores observados para cada acão estão empilhados um sobre o outros, o que geralmente chamamos de dados em formato long. Precisaremos agrupar e transfomá-los no formato wide, o que daremos mais detalhes na sequência.

O terceiro pacote é o highcharter, bastante conhecido por gerar gráficos interativos no formato html. O quarto pacote, pracma é um pacote de funções numéricas que iremos utilizar para gerar números aleatórios e quinto e último pacote, reshape2 irá também nos ajudar no tratamento dos dados. Dessa forma, vamos ao carregamento dessas libraries…

# Pacotes Utilizados no Script
library(BatchGetSymbols)
library(tidyverse)
library(highcharter)
library(pracma)
library(reshape2)
library(widgetframe)

Explicada a razão do uso dos pacotes acima, vamos ao detalhamento dos próximos passos do script. Conforme mencionado anteriormente, a função GetIbovStocks() caputa os símbolos de todas as ações listadas no Ibovespa no momento atual. Todavia, para podermos usar esses tickers para puxar os dados através da BatchGetSymbols() precisamos mergiar no nome do ticker a palavra “.SA”, porque essa é a forma que as ações são listadas no Yahoo Finance.

Sobre a data de início, definimos o primeiro dia de 2010 e a última data a data obtida de nosso sistema, através da função Sys.Date(). Um ponto importante e recomendado é que o parâmetro do.cache seja definido como FALSE. Ela indica se devemos apenas atualizar a base guardada no cache ou baixá-la por completo. Faria sentido usar o cache, todavia em algumas situações ocorre que cria-se dias em duplicidade, o que traz problema posterior para o tratamento dos dados.

Na sequência, separamos no formato wide os retornos diários das ações ajustado para proventos. Conforme anteriormente mencionado, os dados obtidos no download estão no formato de lista e dentro da lista há o dataframe df.tickers. Ali, temos os dados empilhados. Para separá-los por ação, precisamos fazer uso das funções que fazem parte do tydeverse, mais especificamente do dplyr. Tendo sido o pacote carregado, utilizamos o comando %>% após a declaração do comando para apontar que na linha de baixo haverá uso de outra função na sequência tratando os mesmos dados do dataframe. Utilizamos a função select() para escolher as colunas desejadas do dataframe, o group_by() para marcar em grupos as observações na sequência: data, ticker e retorno. Por fim, mudamos o formato de long para wide através da função spread()*. Ela irá gerar uma coluna para cada ticker existente com os valores do retorno separados por data. Na última parte desse pedaço do script, pedimos para calcular a covariância entre os retornos das ações. Repare que nem todas as ações possuem cotações de idêntica janela temporal. Por essa razão fazemos uso do comando “pairwise.complete.obs” para apenas calcular onde houver paremaento de retornos. Os resultados são alocados em uma matriz \(n \times n\).

# Obtenção dos Tickers e Download dos Dados.
df.Ibov    <- GetIbovStocks()
my.tickers <- paste0(df.Ibov$tickers, '.SA')

df.stocks <- BatchGetSymbols(tickers = my.tickers,
                             first.date = '2010-01-01', 
                             last.date = Sys.Date(), do.cache = FALSE)


# Parte que faz uso do pacote dplyr, que faz parte do tydeverse.
Retornos_dia  <- df.stocks$df.tickers %>%
                 select(ref.date, ticker, ret.adjusted.prices)   %>%
                 group_by(ref.date, ticker, ret.adjusted.prices) %>%
                 spread(ticker, ret.adjusted.prices)

# Cálculo da Matriz de Covariância entre os Retornos das Ações
Matriz_Cov <- cov(Retornos_dia[,-1],Retornos_dia[,-1],
                  use = "pairwise.complete.obs")

Tendo sido calculada a matriz de covariância entre os ativos, precisamos agora remover e isolar os dados de variância presentes nessa matriz. É importante lembrar que por definição, a covariância do retorno de uma ação com ela mesma é a sua própria variância. Assim, Repare na matriz abaixo que a diagonal principal representa as variâncias dos ativos, enquanto que os elementos na triangular superior e inferior da matriz representam a covariância entre os ativos do portfólio. Isso é importante para podermos explicar como deve ser caculada a covariância média, \(\overline{\sigma}_{ij}\quad\forall i\neq j\), bem como a variância média, \(\overline{\sigma^2_{i}}\quad i=[1,2,...,n]\). Sobre o número de variância, temos \(n\) variâncias para \(n\) ativos. Já para a covariância, temos \(n\times(n-1)\) covariâncias entre os ativos.

\[Cov(Ret)=\begin{bmatrix}\sigma_{1}^{2} & \sigma_{12} & \ldots & \sigma_{1n}\\ \sigma_{21} & \sigma_{2}^{2} & \cdots & \sigma_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_{n}^{2} \end{bmatrix}\]

Vamos nessa parte detalhar a lógica do script. O Número de ativos é dado pelo número de linhas (ou colunas) da matriz de covariância. Aqui cabe uma nota. Embora o IBOV possua mais de 70 ativos atualmente, nem todos os ativos apresentam elevada liquidez. Com isso, quando usamos o comando para fazer o download das séries, aqueles ativos que possuem menos de 75% de informação acerca das cotações históricas são descartadas. Dando sequência, para extrair a diagonal da matriz de covariância ,ou seja, os dados de variância, necessitamos usar o camdno diag() duas vezes. A primeira para obter os valores e alocar em um vetor \([1\times n]\) e a segunda para criar uma matriz diagonal \([n \times n]\) com esses valores separados no vetor. Para separar a matriz apenas com covariâncias, basta pegar a matriz original e subtrair da nova matriz de variâncias. Obtida a matriz isolada das covariâncias, basta usar a função sum() para somar todos os elementos da matriz. A covariância média passa a ser calculada como: \(2.\sum_{1<i<j<n}\sigma_{ij}/[n.(n-1)]\). O cálculo da variância média é mais direto. Basta utilziar a função mean() sobre a matriz diagonal que armazena as variâncias individuais, ou seja, \(\sum_{i=1}^n \sigma_i^2/n\). Como a covariância média é apenas um número, aproveitamos e criamos um vetor para utilizar posteriormente.

Num_Ativos      <- nrow(Matriz_Cov)
Matriz_Diagonal <- diag(diag(Matriz_Cov))
B               <- Matriz_Cov - Matriz_Diagonal
Soma_Elementos  <- sum(B)
Cov_Med         <- Soma_Elementos/(Num_Ativos*(Num_Ativos-1))

Var_Med       <- mean(diag(Matriz_Cov))

A 1ª Simulação: Carteira Igualmente Dividida Utilizando Medidas de Variância e Covariância Média

Agora antes de darmos sequência com uma figura, vamos explicar a intuição de utilizar medidas como variância média e covariância média. O risco de uma carteira com \(n\) ativos é dada por: \[\sigma_{Port}^2=\sum_{i=1}^na_i^2.\sigma_i^2+2.\sum_{1\leq i\leq j\leq n}a_i.a_j.\sigma_{ij}\] Se cada ativo for igualmente ponderado por fatias iguais, temos que a expressão acima se torna: \[\sigma_{Port}^2=\frac{1}{n^{2}}.\sum_{i=1}^n\sigma_i^2+\frac{2}{n^{2}}.\sum_{1\leq i\leq j\leq n}\sigma_{ij}\] Repare que podemos fatorizar o termo \(1/{n^{2}}\) em \(\frac{(n-1)}{n}.\frac{1}{n.(n-1)}\) e substituir na expressão acima. Assim, obtemos: \[\sigma_{Port}^2=\frac{1}{n}.\overline{\sigma_i^2}+\frac{(n-1)}{n}.\overline{\sigma_{ij}}\] Onde \(\overline{\sigma_i^2}=\sum_{i=1}^n\sigma_i^2/n\) e \(\overline{\sigma_{ij}}=(2.\sum_{1\leq i\leq j\leq n}\sigma_{ij})/[n.(n-1)]\)

Assim, a equação anterior nos permite inferir a variância de um portfólio a partir da variância e covariância média alterando apenas o número de ativos. De maneira muito simples, podemos aplicar o operador limite e verificar que a variância do portfólio converge para a covariância média dos ativos: \[\lim_{n\to\infty}\sigma^2_{Port}=\overline{\sigma_{ij}}\].

É isso que iremos simular na sequência. Já temos o cáculo das variância e covariância média dos ativos. Iremos então criar um vetor com as possibilidade de ativos entre 1 e 150, segmentados a cada uma unidade. Cálculamos a variância do portfólio através da fórmula desenvolvida e podemos ao fim transformá-la em desvio padrão e anualizá-la. Na sequência o plot de duas figuras. A primeira em termos de variância e a segunda em termos de desvio-padrão anualizado.

Ativos        <- seq(from = 1, to = 150, by = 1)

Var_Port      <- (1/Ativos)*Var_Med + (Ativos/(Ativos-1))*Cov_Med
DP_Port       <- Var_Port^(0.5)
DP_Anual_Port <- DP_Port*sqrt(252)

Linha_Cov_Med <- rep(Cov_Med, length(DP_Anual_Port))


### Figura em termos de Variância
frameWidget(highchart(type = "chart") %>% 
  hc_add_series(Var_Port*100, type = "line", 
                name = "Variância do Portfólio x Número de Ativos",
                color = "blue") %>%
  hc_add_series(Linha_Cov_Med*100, type = "line",
                name = "Covariância Média das Ações do Ibovespa",
                color = "black", dashStyle = "longdash") %>%
  hc_title(text = "Variância de um Portfólio versus Número de Ativos", 
         margin = 10,
         style = list(fontSize= "14px")) %>%
  hc_subtitle(text = "Dados Obtidos das Ações do IBOV - 2010 a 2019") %>%
  hc_xAxis(title = list(text = "Número de Ativos")) %>%
  hc_yAxis(title = list(text = "Variância do Portfólio %"),
           labels = list(format = "{value}%")))

Podemos obter o mesmo gráfico sendo medido em termos de desvio padrão…

### Figura em termos de Desvio Padrão
frameWidget(highchart(type = "chart") %>% 
  hc_add_series(DP_Anual_Port*100, type = "line", 
                name = "Desvio-Padrão do Portfólio x Número de Ativos",
                color = "red") %>%
  hc_title(text = "Desvio-Padrão Anual de um Portfólio versus Número de Ativos", 
           margin = 10,
           style = list(fontSize= "14px")) %>%
  hc_subtitle(text = "Dados Obtidos das Ações do IBOV - 2010 a 2019") %>%
  hc_xAxis(title  = list(text = "Número de Ativos")) %>%
  hc_yAxis(title  = list(text = "Desvio-Padrão do Portfólio %"),
           labels = list(format = "{value}%")))

A 2ª Simulação: Carteiras Aleatórias com 54 Ativos

Na parte anterior calculamos a média da variância e covariância e vimos através da figura 1 gerada que a medida que a carteira aumenta o número de ativos, temos a convergência assintótica da variância do portfólio para a covariância média. Todavia, aqui há uma certa premissa forte: que a variância média e a covariância média sejam iguais para todas as carteiras. Iremos agora relaxar essa hipótese e fazer o seguinte: apurar todas as variâncias (e respectivos desvios-padrões) das carteiras que possam ter \(1,2,...,n\) ativos. Testar todas as carteiras não é um exercício simples, uma vez que trata-se de uma cobinação de \(n\) ativos em grupos de \(p\) sendo \(p=[1,2,...,n]\). Isso gerar \(n\) combinações \(C_{n,p}=n!/[p!(n-p)!]\). Quantas possibilidades de carteiras temos para cada número de ações na carteira?

N <- 54 #Número de Ações Totais da Amostra
p <- seq(from = 1, to = N, by = 1) # Número de Ações no Portfólio
Combinacoes <- factorial(N)/(factorial(p)*factorial(N-p))

plot(y = Combinacoes, 
     x = p, 
     type = "b", 
     col = "red",
     lwd = 2,
     main = "Combinação de Carteiras n x p",
     xlab = "Número de Ativos na Carteira (p)",
     ylab = "Número de Combinações Possíveis para (n) ativos")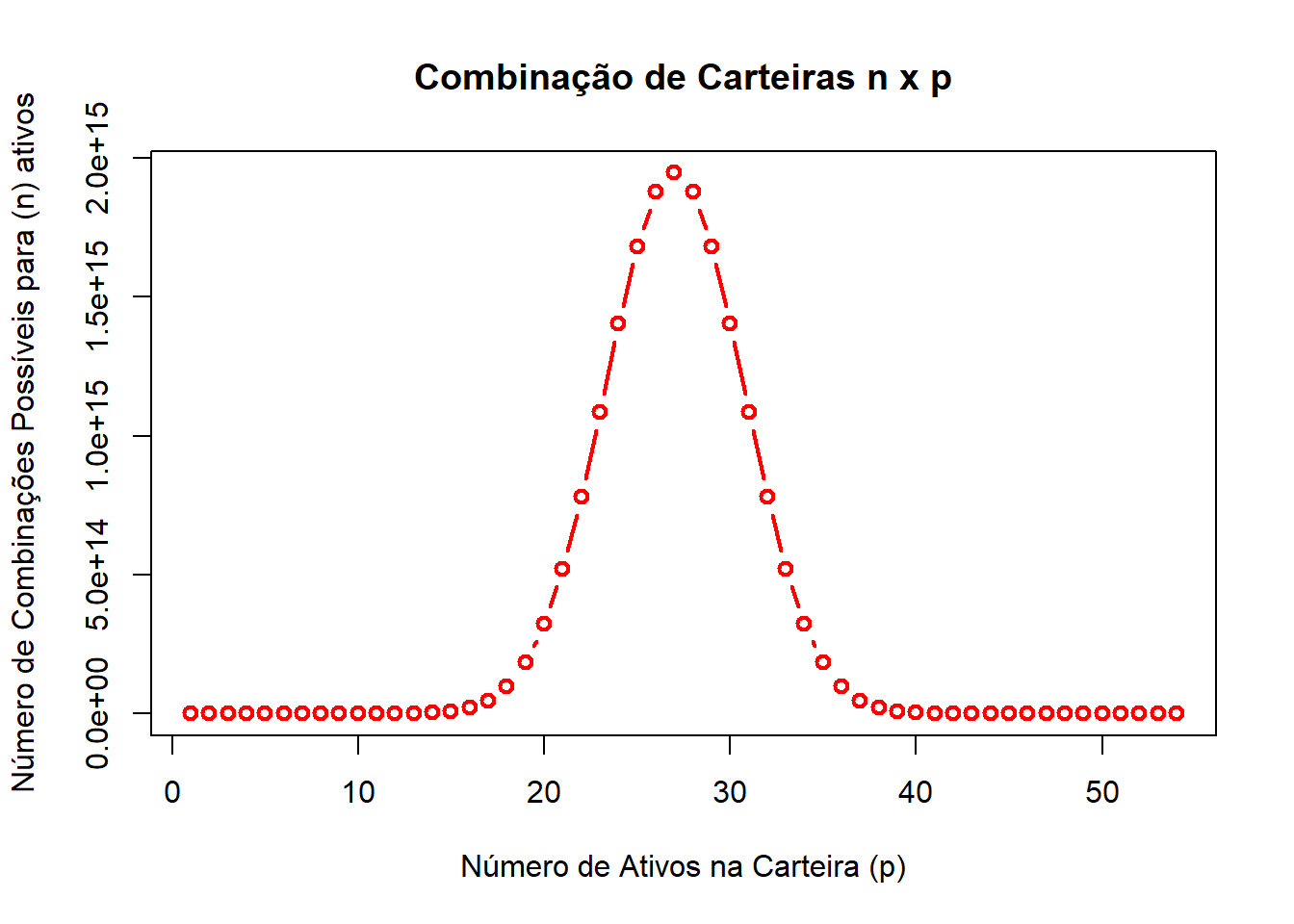

Dessa forma, achamos que quando a carteira é montada com 27 ativos, temos um valor de \(2.0\times e^{15}\) combinações possíveis com os \(54\) ativos existentes. Isso posto, temos que escolher um número de combinações possíveis que não seja tão grande (de modo a ser computacionalmente inviável) e nem tão pequeno para não representar bem os efeitos amostrais. De maneira ad hoc escolhemos 5000 combinações para cada número de ativos.

Dando sequência ao script, fizemos o seguinte: Deixamos limpa de datas a matriz de retorno diária, definimos o número de simulações de possíveis carteiras em \(5.000\), definimos o número de ações da amostra como sendo \(54\) (total que sobram do IBOV com mais de 75% de negociação no período) e pré-alocamos uma matriz com valores em branco (NA) de tamanho: \(5000\) Linhas e \(54\) Colunas.

Isso posto, laçaremos dois loopings: 1) para resolver todas as simulações para \(p\) ativos e; 2) Para resolver de \(p\to N\) ativos. O sorteio das carteiras faz uso da função randperm() que faz parte do pacote pracma. Ela nos permite sortear \(p\) ativos aleatórios na amostra de \(1 a 54\). Feito isso, empilham-se os dados (através da função melt()) e gera-se a figura. Como resultado final, plotamos o risco das carteiras simuladas e a média de risco calculada pelo número de ativos na carteira. Assim, fica claro o ganho obtido na diversificação em termos de queda de variância do portfólio (e desvio-padrão).

Retornos <- Retornos_dia[,-1]
N_Sim    <- 5000
N_Ativos <- 54
Sd       <- matrix(NA, nrow = N_Sim, ncol = N_Ativos)


for (i in 1:N_Ativos) {
for (i2 in 1:N_Sim) {
  
  Index <- randperm(1:54,i)
  Ret   <- rowSums((1/i)*Retornos[,Index], na.rm = T)
  Sd[i2,i] <- sd(Ret)*sqrt(252)
  
}}

Med_linha <- colMeans(Sd)
Med_linha <- data.frame(cbind(Med_linha,seq(from = 1, to = N_Ativos, by = 1)))

a <- melt(Sd)
a1 <- a[,-1]


frameWidget(highchart() %>%
  hc_add_series(a1, "scatter", hcaes(x = Var2, y = value*100), color = "cyan", 
                name = "Carteiras Sorteadas") %>%
  hc_add_series(Med_linha, "line", hcaes(x = V2, y = Med_linha*100), 
                color = "black", name = "Média das Carteiras") %>%
  hc_title(text = "Desvio-Padrão Anual de um Portfólio versus Número de Ativos", 
           margin = 10,
           style = list(fontSize= "14px")) %>%
  hc_subtitle(text = "Dados Obtidos das Ações do IBOV - 2010 a 2019") %>%
  hc_xAxis(title  = list(text = "Número de Ativos")) %>%
  hc_yAxis(title  = list(text = "Desvio-Padrão do Portfólio %"),
           labels = list(format = "{value}%")))

Referências

ALEXANDER, C. Modelos de Mercado. Um Guia para a Análise de Informações Financeiras. BM&FBOVESPA, São Paulo. 2005.

BODIE, Z; KANE, A; MARCUS, A. Fundamentos de Investimentos. 3ª Edição. Editora Bookman. 2008.

CHEN, J. M. Postmodern Portfolio Theory. Navigating Abnormal Markets and Investor Behavior. Palgrave Macmillan. 2016.

ELTON, E. J. et al. Modern Portfolio Theory and Investiment Analysis. 9th Edition. John Wiley & Sons. 2014.