Simulação de Modelos *Stock-Flow Consistent*: Modelo SIM - Godley e Lavoie (2007)
Introdução
A metodologia Stock-Flow Consistent é uma abordagem utilizada em modelos Macrodinâmicos Pós-Keynesianos recentes. Em seu seio, há um tratamento contábil utilizando o princípio de partidas dobradas para que a Moeda seja um passivo do Governo (ou Banco Central) e um ativo para aqueles que a carregam. Nesse sentido, torna-se possível identificar o caminho dos ativos financeiros em uma economia monetária da produção, tal como desenvolvida na teoria Keynesiana.
Além disso, o princípio das partidas dobradas mostra para cada despesa realizada, há uma receita como contraparte, bem como para cada variação de estoque, há um fluxo correspondente. Como o intuito do post é dar ênfase a resolução do modelo, convido os interessados a fazer uma leitura do Capítulo 3 de Godley e Lavoie (2007). Lá há maior detalhamento das premissas utilzadas, bem como a matrizes de Balanço Patrimonial dos agentes e a de Transações.
Equações do Modelo
\[C_s = C_d\] \[G_s = G_d\] \[T_s = T_d\] \[N_s = N_d\] \[Yd = W.N_s - T_s\] \[T_d = \theta.W.N_s\] \[C_d =\alpha_1 . Yd + \alpha_2 . H_h[t-1]\] \[H_s = H_s[t-1] + G_d - T_d\] \[H_h = H_h[t-1] + Yd - C_d\] \[Y = C_s + G_s\] \[N_d = Y/W\] onde os subscritos \(d,s\) e \(h\) representam demandado, ofertado e das famílias; \([t-1]\) faz referência a variável defasada; as variáveis são: Consumo das Famílias, \(C\), Consumo do Governo, \(G\), Tributos, \(T\), Trabalho, \(N\), Renda Disponível, \(Yd\), Moeda, \(H\), Produção, \(Y\) e por fim, Salários, \(W\). Algumas restrições aos parâmetros: \(0<\alpha_2<\alpha_1<1\) e \(0<\theta<1\).
O Estado Estacionário do Modelo
Para tratar o estado estacionário do Modelo SIM, podemos verificar alguns pontos:
- Tanto \(H_s^*\) quanto \(H_d^*\) são indeterminados (por essa equações). Todavia, as mesmas equações garantem que: \(G_d^*=T_d^*\) e \(Yd^*=Cd^*\)
- Como \(Yd=(1-\theta).Y\) e \(Y=C_d+G_d\), necessariamente temos que: \(Y^*=(1/\theta).G_d^*\)
- Cuidado! Não confundir o equilíbrio de curto-prazo, dado por \(Y=G_d/[1-\alpha_1.(1-\theta)]\), com o equilíbrio de estado estacionário! O de curto prazo é uma aplicação direta do componente autônomo vezes o multiplicador keynesiano tradicional.
Simulação
A primeira parte do script serve como preparação para a simulação. Nela devemos inserir os valores dos parâmetros, estoques iniciais, valor das variáveis exógenas e tempo de simulação.
Antes de começar, usamos o comando rm(list=ls()) para limpar as variáveis que estejam previamente carregadas no R. Além disso, iremos usar apenas um pacote latex2exp para poder utilizar expressões matemática em latex no gráfico.
Um ponto importante que cabe destaque no script abaixo é que para cada variável endógena do sistema, teremos que fazer uma pré-alocação de um vetor com valores zerados. Isso é feito através da função vector(). O tamanho do vetor é similar ao número de observações temporais. Com relação a parte de variáveis exógenas, deixamos G_d como um vetor repetido com valores de 25 unidades (gasto público constante) e o salário nominal W como escalar de valor 1.
### SIM Model - Godley and Lavoie
rm(list=ls())
library(latex2exp)
Tempo <- 50
### Pré-alocação de variáveis endógenas.
C_s <- vector(length = Tempo, mode = "numeric")
C_d <- vector(length = Tempo, mode = "numeric")
G_s <- vector(length = Tempo, mode = "numeric")
G_d <- vector(length = Tempo, mode = "numeric")
H_s <- vector(length = Tempo, mode = "numeric")
H_h <- vector(length = Tempo, mode = "numeric")
N_s <- vector(length = Tempo, mode = "numeric")
N_d <- vector(length = Tempo, mode = "numeric")
Yd <- vector(length = Tempo, mode = "numeric")
Y <- vector(length = Tempo, mode = "numeric")
W <- vector(length = Tempo, mode = "numeric")
T_s <- vector(length = Tempo, mode = "numeric")
T_d <- vector(length = Tempo, mode = "numeric")
# Parâmetros
alpha_1 <- 0.6
alpha_2 <- 0.4
theta <- 0.2
# Variáveis Exógenas
G_d <- rep(20, Tempo)
W <- 1
# Valores Iniciais
H_s[1] <- 0
H_h[1] <- 0A segunda parte do script tem a finalidade de resolver o sistema no tempo (equilíbrio simultâneo das equações) quando ao longo do tempo (iteração com o tempo rolando). A forma com que está no script é uma alternativa bastante simples para a resolução do modelo. Alternativamente poderíamos utilizar explicitamente o algoritmo de Gauss-Seidel para resolução do sistema, bem como o pacote PKSFC desenvolvido por Antoine Godin1. Além da resolução, ao fim calculamos o valor teórico de Steady-State para \(Y^*\).
# Resolução do Modelo
for (i in 1:Tempo) {
if (i == 1) {
for (iterations in 1:100){
}}
else {
for (iterations in 1:100){
C_s[i] = C_d[i]
G_s[i] = G_d[i]
T_s[i] = T_d[i]
N_s[i] = N_d[i]
Yd [i] = W*N_s[i] - T_s[i]
T_d[i] = theta*W*N_s[i]
C_d[i] = alpha_1*Yd[i] + alpha_2*H_h[i-1]
H_s[i] = H_s[i-1] + G_d[i] - T_d[i]
H_h[i] = H_h[i-1] + Yd[i] - C_d[i]
Y [i] = C_s[i] + G_s[i]
N_d[i] = Y[i]/W
}}}
# Y de Estado Estacionário
Y_ast <- G_d/thetaPor fim, plotamos algumas trajetórias e constatamos a convergência para o estado estacionário, conforme apontado analiticamente. A respeito da estabilidade do modelo, iremos abordar em outro post!
# Plot das Figuras
plot(1:Tempo,Y, main = "PIB - Modelo SIM", type = "l",
xlab = "Tempo Simulado", ylab = "Valor Monetário", lwd = 2)
lines(1:Tempo, Y_ast, lty = 2, lwd = 2, col = "red")
grid(nx = NULL, ny = NULL, lty = "dotted", col = "grey")
legend("bottomright", c("Y",TeX("$\\Y^*$ - Estado Estacionário")), inset = 0.05,
lwd = "2", lty = c(1,2), cex = 0.9, col = c("black","red"))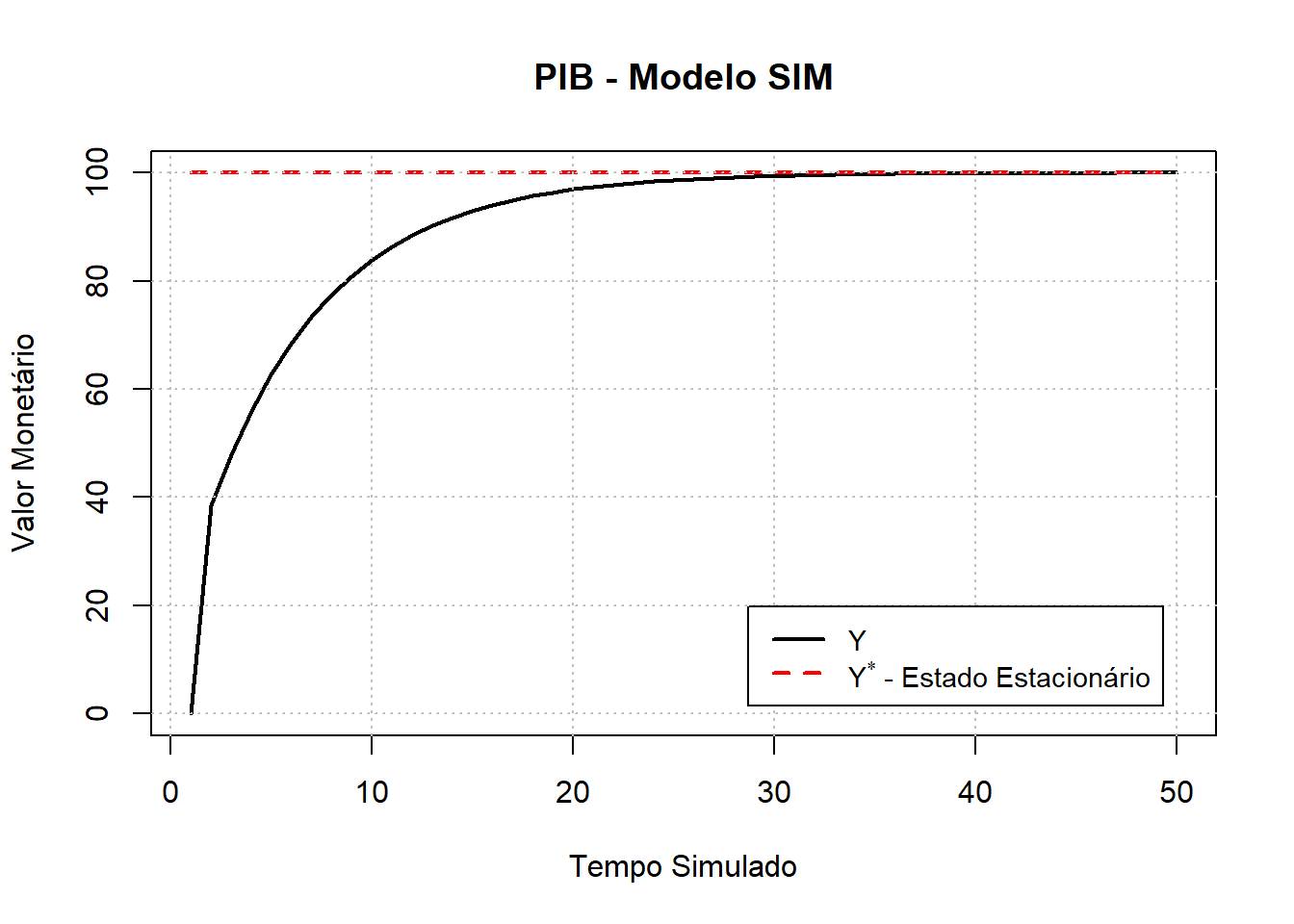
plot(1:Tempo,G_d, main = "Tributos e Gasto Público - Modelo SIM", type = "l",
xlab = "Tempo Simulado", ylab = "Valor Monetário", lwd = 2,
ylim = c(0,20), col = "magenta")
lines(1:Tempo, T_d, lty = 2, lwd = 2, col = "blue")
grid(nx = NULL, ny = NULL, lty = "dotted", col = "grey")
legend("bottomright", c(TeX("$\\G_d^*$"),TeX("$\\T_d^*$")), inset = 0.05,
lwd = "2", lty = c(1,2), cex = 0.9, col = c("magenta","blue"))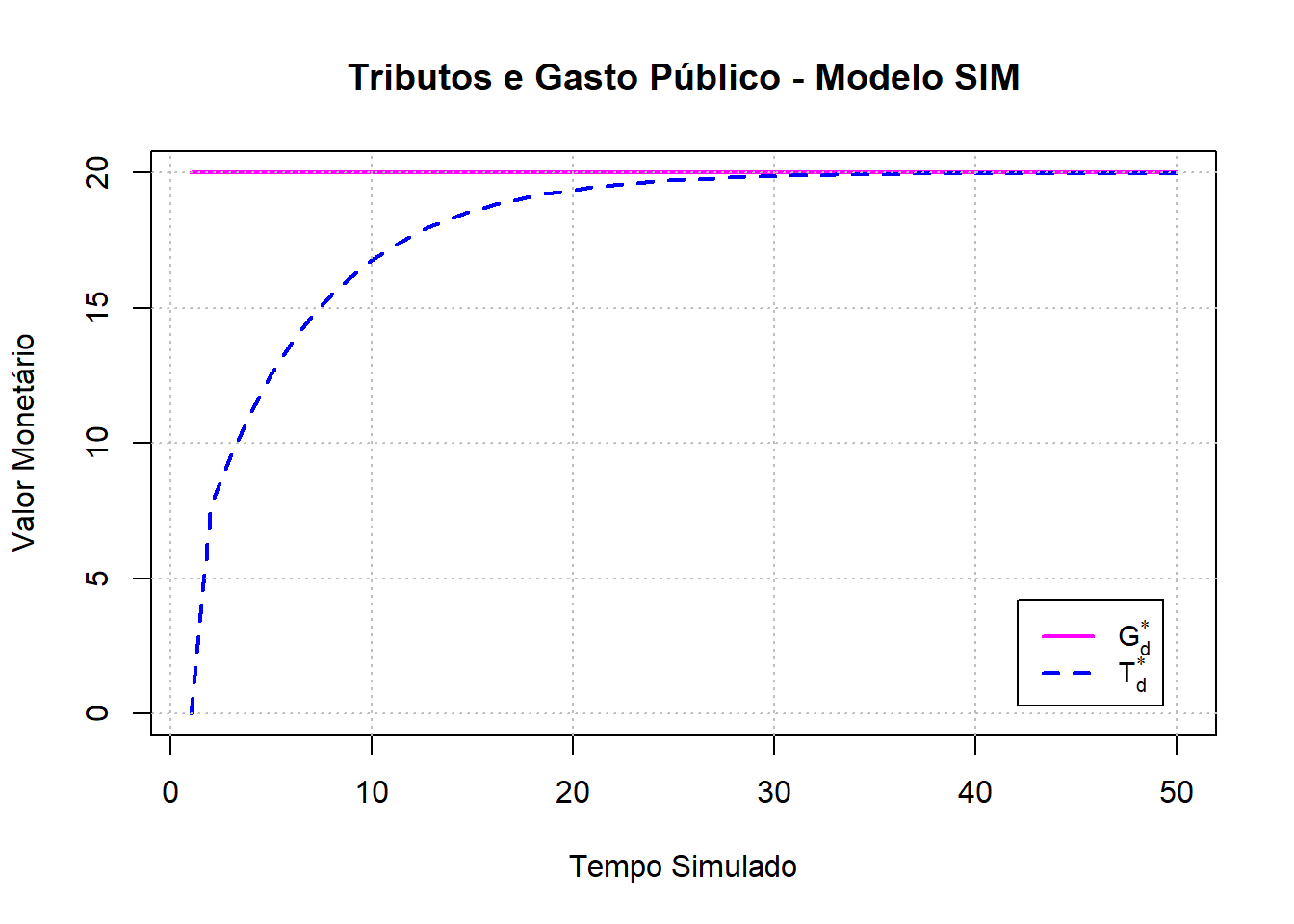
plot(1:Tempo,C_d, main = "Consumo e Renda Disponível - Modelo SIM", type = "l",
xlab = "Tempo Simulado", ylab = "Valor Monetário", lwd = 2,
ylim = c(0,90), col = "green")
lines(1:Tempo, Yd, lty = 2, lwd = 2, col = "cyan")
grid(nx = NULL, ny = NULL, lty = "dotted", col = "grey")
legend("bottomright", c(TeX("$\\C_d^*$"),TeX("$\\Yd^*$")), inset = 0.05,
lwd = "2", lty = c(1,2), cex = 0.9, col = c("green","cyan"))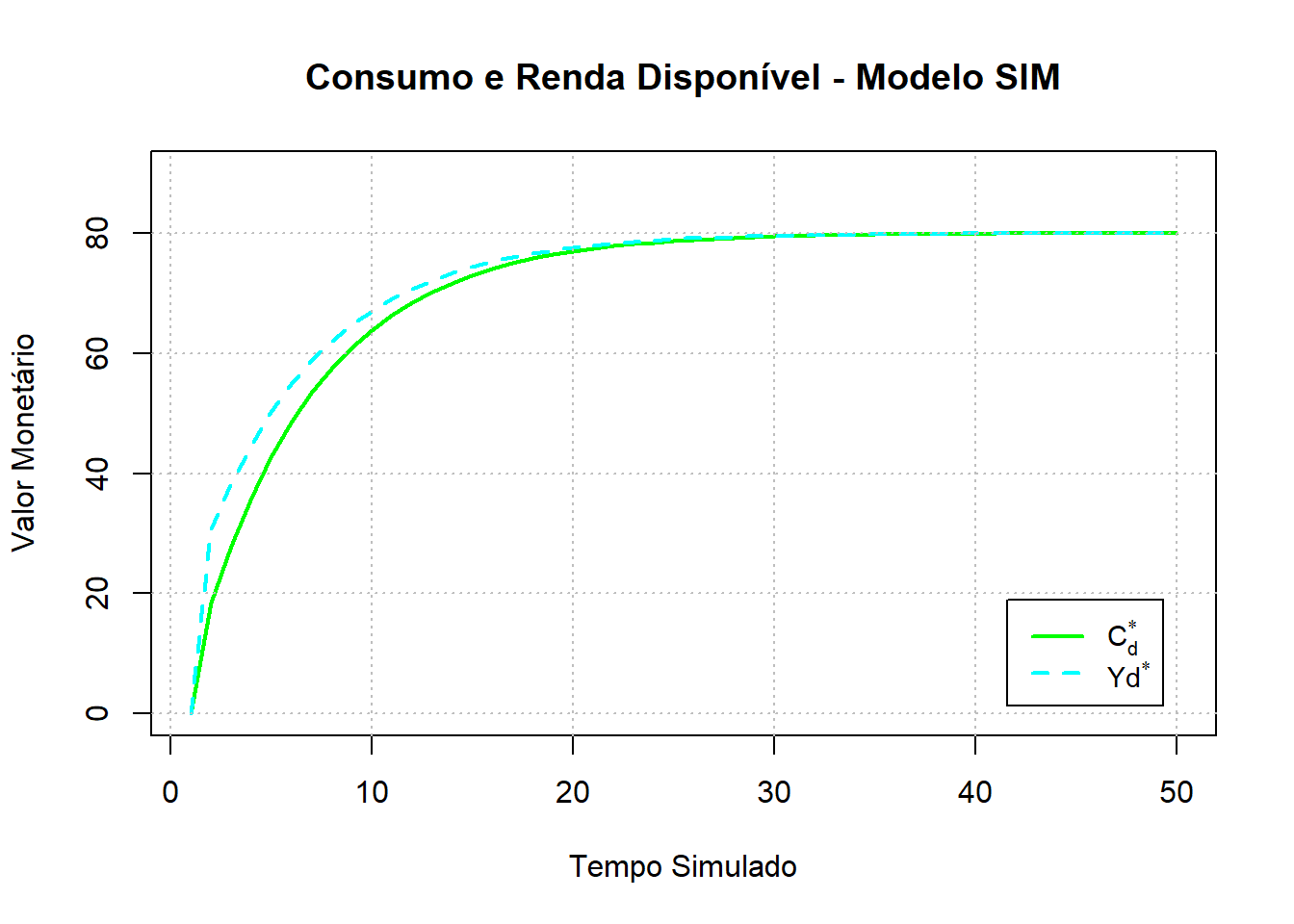
Tabelando os dados
Nesta parte, apenas juntamos os vetores em um data.frame, arredondamos os valores numéricos para duas casas decimais e plotamos em uma tabela no formato html. A primeira coluna é o eixo do tempo de simulação. Através do comando tail, selecionamos para serem exibidas as últimas 15 observações de cada vetor. Para gerar a tabela, fizemos uso da função kable que pertence ao pacote kableExtra.
library(kableExtra)
Tabela_Final <- data.frame(
round(cbind(C_s,C_d,G_s,G_d,H_s,H_h,N_s,N_d,Yd,Y,W,T_s,T_d), digits = 2))
kable(tail(Tabela_Final, 15)) %>%
kable_styling(bootstrap_options = c("striped", "hover"))| C_s | C_d | G_s | G_d | H_s | H_h | N_s | N_d | Yd | Y | W | T_s | T_d | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 36 | 79.79 | 79.79 | 20 | 20 | 79.77 | 79.77 | 99.79 | 99.79 | 79.83 | 99.79 | 1 | 19.96 | 19.96 |
| 37 | 79.82 | 79.82 | 20 | 20 | 79.80 | 79.80 | 99.82 | 99.82 | 79.86 | 99.82 | 1 | 19.96 | 19.96 |
| 38 | 79.85 | 79.85 | 20 | 20 | 79.83 | 79.83 | 99.85 | 99.85 | 79.88 | 99.85 | 1 | 19.97 | 19.97 |
| 39 | 79.87 | 79.87 | 20 | 20 | 79.86 | 79.86 | 99.87 | 99.87 | 79.90 | 99.87 | 1 | 19.97 | 19.97 |
| 40 | 79.89 | 79.89 | 20 | 20 | 79.88 | 79.88 | 99.89 | 99.89 | 79.91 | 99.89 | 1 | 19.98 | 19.98 |
| 41 | 79.91 | 79.91 | 20 | 20 | 79.90 | 79.90 | 99.91 | 99.91 | 79.93 | 99.91 | 1 | 19.98 | 19.98 |
| 42 | 79.92 | 79.92 | 20 | 20 | 79.92 | 79.92 | 99.92 | 99.92 | 79.94 | 99.92 | 1 | 19.98 | 19.98 |
| 43 | 79.93 | 79.93 | 20 | 20 | 79.93 | 79.93 | 99.93 | 99.93 | 79.95 | 99.93 | 1 | 19.99 | 19.99 |
| 44 | 79.94 | 79.94 | 20 | 20 | 79.94 | 79.94 | 99.94 | 99.94 | 79.96 | 99.94 | 1 | 19.99 | 19.99 |
| 45 | 79.95 | 79.95 | 20 | 20 | 79.95 | 79.95 | 99.95 | 99.95 | 79.96 | 99.95 | 1 | 19.99 | 19.99 |
| 46 | 79.96 | 79.96 | 20 | 20 | 79.96 | 79.96 | 99.96 | 99.96 | 79.97 | 99.96 | 1 | 19.99 | 19.99 |
| 47 | 79.97 | 79.97 | 20 | 20 | 79.96 | 79.96 | 99.97 | 99.97 | 79.97 | 99.97 | 1 | 19.99 | 19.99 |
| 48 | 79.97 | 79.97 | 20 | 20 | 79.97 | 79.97 | 99.97 | 99.97 | 79.98 | 99.97 | 1 | 19.99 | 19.99 |
| 49 | 79.98 | 79.98 | 20 | 20 | 79.97 | 79.97 | 99.98 | 99.98 | 79.98 | 99.98 | 1 | 20.00 | 20.00 |
| 50 | 79.98 | 79.98 | 20 | 20 | 79.98 | 79.98 | 99.98 | 99.98 | 79.98 | 99.98 | 1 | 20.00 | 20.00 |
Referências
GODLEY, W.; LAVOIE, M. Monetary Economics. An Integrated Approach to Credit, Money, Income, Production and Wealth. Palgrave Macmillan. Nova Iorque, EUA. 2007.