Modelo SFC Simples Usando Dados Reais da Economia Norte-Americana (Dafermos e Nikolaidi) - Parte 2/3
Introdução
No post anterior apresentamos o modelo simplificado de Nikolaidi e Dafermos que iremos utilizar para calibrar utilizando dados da economia Norte-Americana. A ideia desse segundo post é justamente resolver o modelo através das distintas formas de calibração e na sequência, simulá-lo.
Na primeira parte do script abaixo, começamos limpando a área de trabalho através do comando rm(list=ls()). Na sequência definimos o tempo de simulação. Fazemos a leitura dos dados tipo “.csv” direto do link do Dropbox dos autores citados. Na sequência, tabelamos os dados reais para verificar e, posteriormente, alocamos vetores numéricos para cada variável endógena que será utilizada no modelo.
# Limpeza e definição do horizonte temporal de Simulação
rm(list=ls())
Tempo <- 51
#Download dos Dados do Dropbox
Data <- read.csv("https://www.dropbox.com/s/kusoabl4s8clhvj/data_dafnik.csv?dl=1")
#Tabulação dos Dados Reais
library(kableExtra)
kable(round(tail(Data, 15), digits = 2)) %>%
kable_styling(bootstrap_options = c("striped", "hover"))| Year | Y | u | rm | rl | sw | gk | gy | K | L | lev | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 1996 | 10.56 | 0.82 | 0.05 | 0.08 | 0.45 | 0.03 | 0.04 | 33.67 | 5.85 | 0.17 |
| 38 | 1997 | 11.04 | 0.83 | 0.06 | 0.08 | 0.45 | 0.03 | 0.04 | 34.70 | 6.24 | 0.18 |
| 39 | 1998 | 11.53 | 0.82 | 0.06 | 0.08 | 0.46 | 0.03 | 0.04 | 35.85 | 6.88 | 0.19 |
| 40 | 1999 | 12.07 | 0.80 | 0.05 | 0.08 | 0.46 | 0.04 | 0.05 | 37.12 | 7.53 | 0.20 |
| 41 | 2000 | 12.56 | 0.80 | 0.06 | 0.09 | 0.46 | 0.04 | 0.04 | 38.44 | 8.04 | 0.21 |
| 42 | 2001 | 12.68 | 0.74 | 0.04 | 0.07 | 0.46 | 0.03 | 0.01 | 39.63 | 8.21 | 0.21 |
| 43 | 2002 | 12.91 | 0.73 | 0.02 | 0.05 | 0.45 | 0.03 | 0.02 | 40.68 | 8.28 | 0.20 |
| 44 | 2003 | 13.27 | 0.74 | 0.01 | 0.04 | 0.44 | 0.03 | 0.03 | 41.79 | 8.22 | 0.20 |
| 45 | 2004 | 13.77 | 0.76 | 0.02 | 0.04 | 0.44 | 0.03 | 0.04 | 43.02 | 8.49 | 0.20 |
| 46 | 2005 | 14.23 | 0.78 | 0.04 | 0.06 | 0.43 | 0.03 | 0.03 | 44.36 | 8.88 | 0.20 |
| 47 | 2006 | 14.61 | 0.79 | 0.05 | 0.08 | 0.43 | 0.03 | 0.03 | 45.67 | 9.48 | 0.21 |
| 48 | 2007 | 14.87 | 0.79 | 0.05 | 0.08 | 0.44 | 0.03 | 0.02 | 46.84 | 10.39 | 0.22 |
| 49 | 2008 | 14.83 | 0.75 | 0.03 | 0.05 | 0.45 | 0.02 | 0.00 | 47.78 | 10.79 | 0.23 |
| 50 | 2009 | 14.42 | 0.66 | 0.01 | 0.03 | 0.44 | 0.01 | -0.03 | 48.25 | 10.16 | 0.21 |
| 51 | 2010 | 14.78 | 0.71 | 0.00 | 0.03 | 0.43 | 0.01 | 0.02 | 48.73 | 9.89 | 0.20 |
# Variáveis Endógenas
W <- vector(length=Tempo, mode = "numeric")
Yc <- vector(length=Tempo, mode = "numeric")
CO <- vector(length=Tempo, mode = "numeric")
D <- vector(length=Tempo, mode = "numeric")
Y <- vector(length=Tempo, mode = "numeric")
TP <- vector(length=Tempo, mode = "numeric")
RP <- vector(length=Tempo, mode = "numeric")
DP <- vector(length=Tempo, mode = "numeric")
I <- vector(length=Tempo, mode = "numeric")
K <- vector(length=Tempo, mode = "numeric")
L <- vector(length=Tempo, mode = "numeric")
BP <- vector(length=Tempo, mode = "numeric")
D_red <- vector(length=Tempo, mode = "numeric")
Y_star <- vector(length=Tempo, mode = "numeric") #Variável Auxiliar
u <- vector(length=Tempo, mode = "numeric") #Variável Auxiliar
gy <- vector(length=Tempo, mode = "numeric") #Variável Auxiliar
lev <- vector(length=Tempo, mode = "numeric") #Variável AuxiliarRepare que, ao fim, também iremos utilizar as variáveis auxiliares. Essas, por definição, são aquelas que não são necessárias para a resolução direta do modelo.
Parte 2 - Definição dos Parâmetros e Simulação do Modelo
Na sequência, resolveremos o modelo. A lógica de resolução é dividida em três partes. A primeira é para resolver o modelo por iteração ao longo do horizonte temporal. A segunda é para calibrar os parâmetros e estoques iniciais no período \(t=1\). A terceira é para resolver o sistema de equações para cada período no tempo.
Iterações de Resolução
- Resolução ao longo do tempo:
for (i in 1:Tempo) {} - Calibração dos Parâmetros e Estoques Iniciais:
if (i == 1){for (iterations in 1:10){} - Resolução das Equações Simultâneas para cada período no tempo:
else {for (iterations in 1:10){}}
Sobre os métodos de calibração dos parâmetros, recomendo a prévia leitura do post anterior. Podemos verificar que utilizamos valores médios, valores de um determinado período
#Parâmetros
for (i in 1:Tempo) {
if (i == 1){
for (iterations in 1:10){
# Parâmetros
sw <- mean(Data[,c("sw")])
rm <- mean(Data[,c("rm")])
rl <- mean(Data[,c("rl")])
c1 <- 0.90
c2 <- 0.75
v <- Y[i]/(K[i]*u[i])
gk <- mean(Data[,c("gy")])
c3 <- (K[i]/L[i])*((Y[i]/K[i])*(1+gk)-gk-(c1*W[i]/K[i]+c2*Yc[i]/K[i]))
sf <- (gk-gk*(L[i]/K[i]))/(TP[i]/(K[i]/(1+gk)))
# Valores Iniciais
u[i] <- Data[1,c("u")]
Y[i] <- Data[1,c("Y")]
K[i] <- Data[1,c("K")]
L[i] <- Data[1,c("L")]
W[i] <- sw*Y[i]
Yc[i] <- DP[i]+BP[i]+rm*(D[i]/(1+gk))
CO[i] <- Y[i]-I[i]
TP[i] <- Y[i]-W[i]-rl*(L[i]/(1+gk))
RP[i] <- sf*TP[i]
DP[i] <- TP[i]-RP[i]
I[i] <- (gk/(1+gk))*K[i]
BP[i] <- rl*(L[i]/(1+gk))-rm*(D[i]/(1+gk))
D[i] <- L[i]
Y_star[i] <- v*K[i]
lev[i] <- L[i]/K[i]
gy[i] <- gk
}}
#Equações
else {
for (iterations in 1:10){
# Famílias
W[i] <- sw*Y[i]
Yc[i] <- DP[i]+BP[i]+rm*D[i-1]
CO[i] <- c1*W[i-1]+c2*Yc[i-1]+c3*D[i-1]
D[i] <- D[i-1]+W[i]+Yc[i]-CO[i]
# Empresas
Y[i] <- CO[i]+I[i]
TP[i] <- Y[i]-W[i]-rl*L[i-1]
RP[i] <- sf*TP[i]
DP[i] <- TP[i]-RP[i]
I[i] <- gk*K[i-1]
K[i] <- K[i-1]+I[i]
L[i] <- L[i-1]+I[i]-RP[i]
# Bancos
BP[i] <- rl*L[i-1]-rm*D[i-1]
D_red[i] <- L[i]
# Equações Auxiliares
Y_star[i] <- v*K[i]
u[i] <- Y[i]/Y_star[i]
gy[i] <- (Y[i]-Y[i-1])/Y[i-1]
lev[i] <- L[i]/K[i]
}}}Resolvido o modelo para que esteja em equilíbrio em cada período no tempo e ao longo do tempo, vamos agora tabelar os resultados. Para isso, utilizaremos a função kable da library(kableExtra). Tabelaremos apenas as últimas 15 observações finais.
library(kableExtra)
Tabela_Final <- data.frame(
round(cbind(W,Yc,CO,D,D_red,TP,RP,DP,I,K,L,BP,u,gy,lev,Y,Y_star), digits = 2))
kable(tail(Tabela_Final, 15)) %>%
kable_styling(bootstrap_options = c("striped", "hover"))| W | Yc | CO | D | D_red | TP | RP | DP | I | K | L | BP | u | gy | lev | Y | Y_star | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 4.52 | 4.24 | 8.65 | 3.54 | 3.54 | 4.81 | 0.83 | 3.98 | 0.94 | 30.55 | 3.54 | 0.05 | 0.8 | 0.03 | 0.12 | 9.60 | 11.98 |
| 38 | 4.67 | 4.38 | 8.93 | 3.66 | 3.66 | 4.96 | 0.86 | 4.10 | 0.97 | 31.52 | 3.66 | 0.05 | 0.8 | 0.03 | 0.12 | 9.90 | 12.36 |
| 39 | 4.81 | 4.52 | 9.21 | 3.77 | 3.77 | 5.12 | 0.89 | 4.23 | 1.00 | 32.53 | 3.77 | 0.05 | 0.8 | 0.03 | 0.12 | 10.22 | 12.76 |
| 40 | 4.97 | 4.66 | 9.51 | 3.89 | 3.89 | 5.28 | 0.91 | 4.37 | 1.03 | 33.56 | 3.89 | 0.05 | 0.8 | 0.03 | 0.12 | 10.54 | 13.16 |
| 41 | 5.13 | 4.81 | 9.81 | 4.02 | 4.02 | 5.45 | 0.94 | 4.51 | 1.07 | 34.63 | 4.02 | 0.05 | 0.8 | 0.03 | 0.12 | 10.88 | 13.58 |
| 42 | 5.29 | 4.96 | 10.12 | 4.14 | 4.14 | 5.62 | 0.97 | 4.65 | 1.10 | 35.73 | 4.14 | 0.06 | 0.8 | 0.03 | 0.12 | 11.22 | 14.01 |
| 43 | 5.46 | 5.12 | 10.44 | 4.28 | 4.28 | 5.80 | 1.00 | 4.80 | 1.14 | 36.87 | 4.28 | 0.06 | 0.8 | 0.03 | 0.12 | 11.58 | 14.46 |
| 44 | 5.63 | 5.28 | 10.78 | 4.41 | 4.41 | 5.99 | 1.04 | 4.95 | 1.17 | 38.04 | 4.41 | 0.06 | 0.8 | 0.03 | 0.12 | 11.95 | 14.92 |
| 45 | 5.81 | 5.45 | 11.12 | 4.55 | 4.55 | 6.18 | 1.07 | 5.11 | 1.21 | 39.25 | 4.55 | 0.06 | 0.8 | 0.03 | 0.12 | 12.33 | 15.39 |
| 46 | 5.99 | 5.62 | 11.47 | 4.70 | 4.70 | 6.37 | 1.10 | 5.27 | 1.25 | 40.50 | 4.70 | 0.06 | 0.8 | 0.03 | 0.12 | 12.72 | 15.88 |
| 47 | 6.18 | 5.80 | 11.84 | 4.85 | 4.85 | 6.58 | 1.14 | 5.44 | 1.29 | 41.78 | 4.85 | 0.06 | 0.8 | 0.03 | 0.12 | 13.12 | 16.39 |
| 48 | 6.38 | 5.99 | 12.21 | 5.00 | 5.00 | 6.79 | 1.17 | 5.61 | 1.33 | 43.11 | 5.00 | 0.07 | 0.8 | 0.03 | 0.12 | 13.54 | 16.91 |
| 49 | 6.58 | 6.18 | 12.60 | 5.16 | 5.16 | 7.00 | 1.21 | 5.79 | 1.37 | 44.48 | 5.16 | 0.07 | 0.8 | 0.03 | 0.12 | 13.97 | 17.44 |
| 50 | 6.79 | 6.37 | 13.00 | 5.32 | 5.32 | 7.22 | 1.25 | 5.97 | 1.41 | 45.90 | 5.32 | 0.07 | 0.8 | 0.03 | 0.12 | 14.42 | 18.00 |
| 51 | 7.01 | 6.58 | 13.42 | 5.49 | 5.49 | 7.45 | 1.29 | 6.16 | 1.46 | 47.36 | 5.49 | 0.07 | 0.8 | 0.03 | 0.12 | 14.88 | 18.57 |
Na sequência, os plots das séries do modelo.
#Gráficos
plot(Data[1:Tempo,c("lev")], type="l", xlab= "Ano", ylab= "Grau de Alavancagem", xaxt="n")
lines(Tabela_Final[1:Tempo,c("lev")], type="l", lty=3)
axis(side=1, at=c(1,11,21,31,41, 51), labels=c("1960","1970","1980","1990","2000","2010"))
legend("bottomright", legend=c("Observado", "Simulado"), lty=c(1,3), bty="n")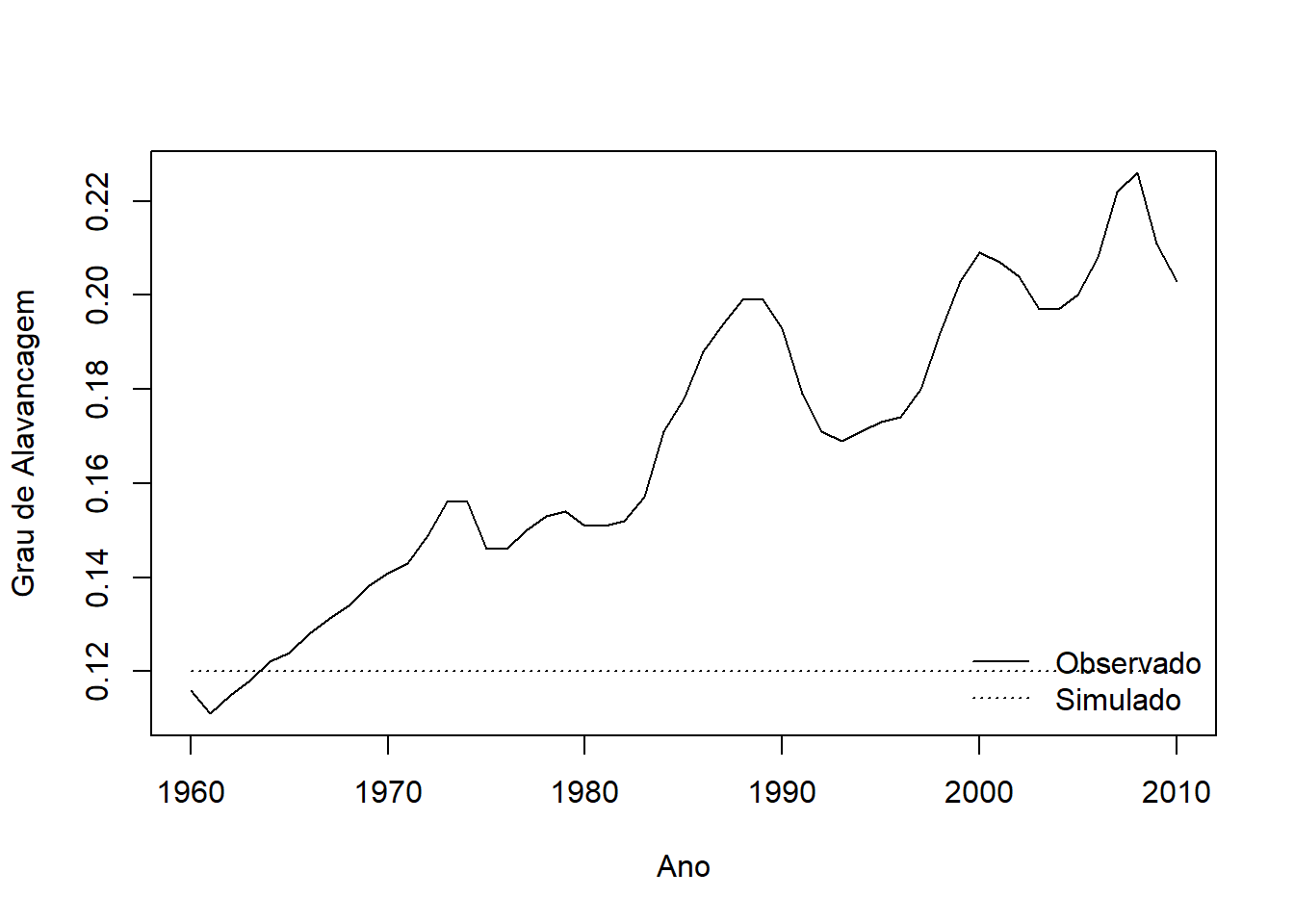
plot(Data[1:Tempo,c("u")], type="l", xlab= "Ano", ylab= "Grau de Utilização da Capacidade Produtiva", xaxt="n")
lines(Tabela_Final[1:Tempo,c("u")], type="l", lty=3)
axis(side=1, at=c(1,11,21,31,41, 51), labels=c("1960","1970","1980", "1990","2000","2010"))
legend("bottomright", legend=c("Observado", "Simulado"), lty=c(1,3), bty="n")
plot(Data[1:Tempo,c("gy")], type="l", lty=1, xlab= "Ano", ylab= "Taxa de Crescimento do Produto", xaxt="n")
lines(Tabela_Final[1:Tempo,c("gy")], type="l", lty=3)
axis(side=1, at=c(1,11,21,31,41, 51), labels=c("1960","1970","1980", "1990","2000","2010"))
legend("bottomright", legend=c("Observado", "Simulado"), lty=c(1,3), bty="n")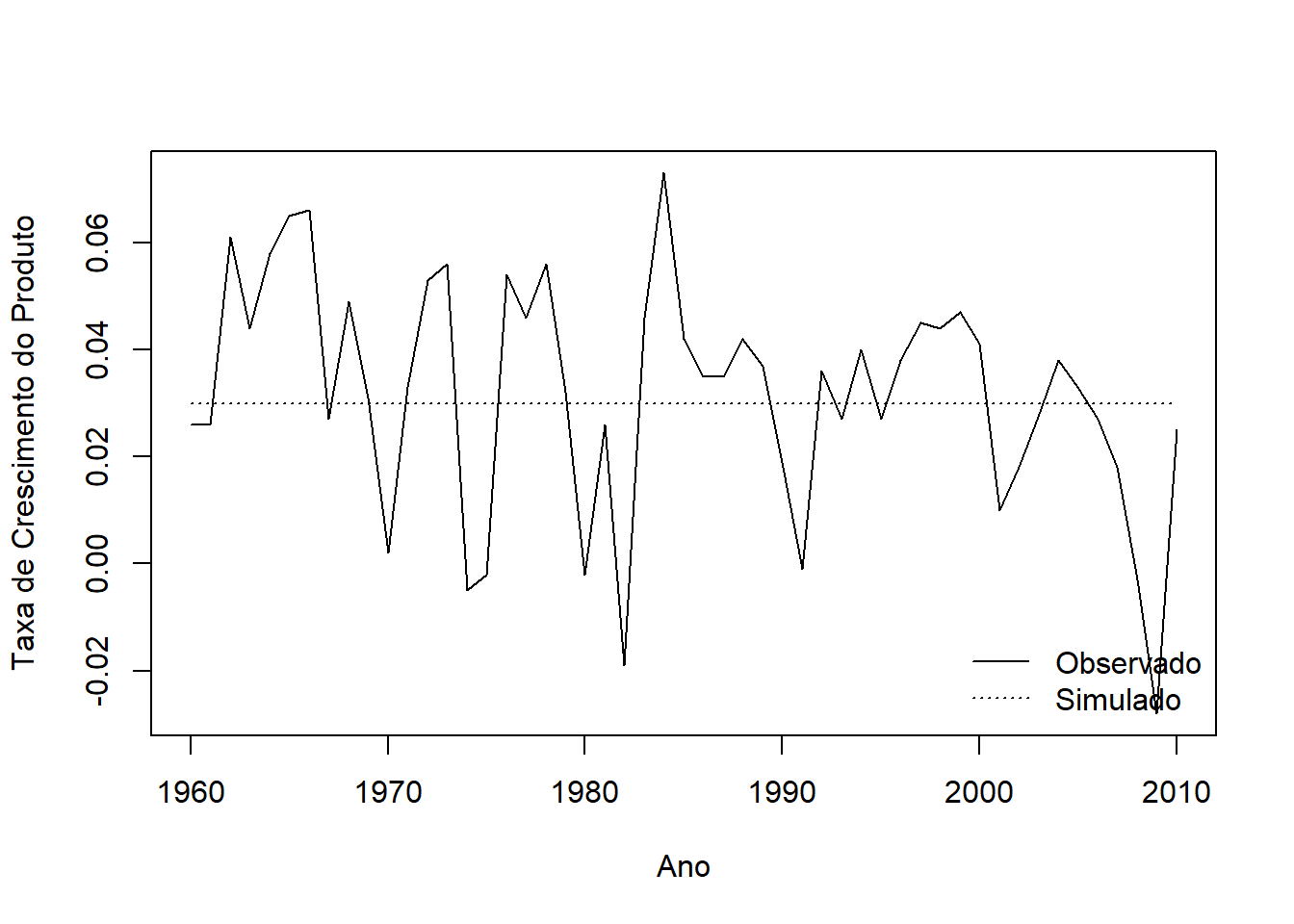
plot(Data[1:Tempo,c("Y")], type="l", lty=1, xlab= "Ano", ylab= "Produto", xaxt="n")
lines(Tabela_Final[1:Tempo,c("Y")], type="l", lty=3 )
axis(side=1, at=c(1,11,21,31,41, 51), labels=c("1960","1970","1980", "1990","2000","2010"))
legend("bottomright", legend=c("Observado", "Simulado"), lty=c(1,3), bty="n")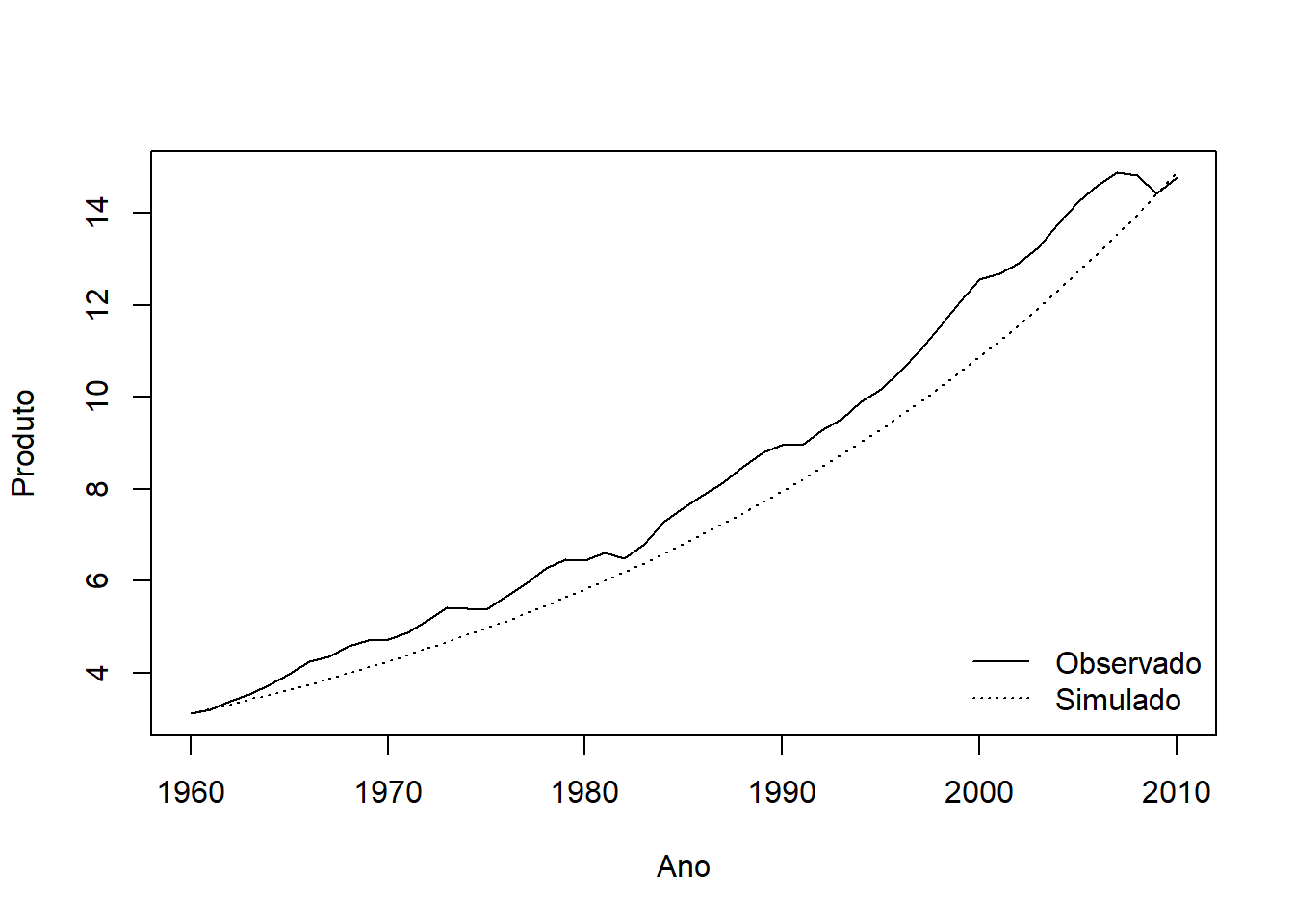
###########################################
#Model validation
#Install.packages("mFilter") #This command is necessary if mFilter has not been installed in your computer
library(mFilter)
Y_log<-log((Tabela_Final[,c("Y")]))
Yactual_log<-log((Data[,c("Y")]))
Y.hp <- hpfilter((Y_log), freq=100, drift=TRUE)
actualY.hp <- hpfilter((Yactual_log), freq=6.25, drift=TRUE)
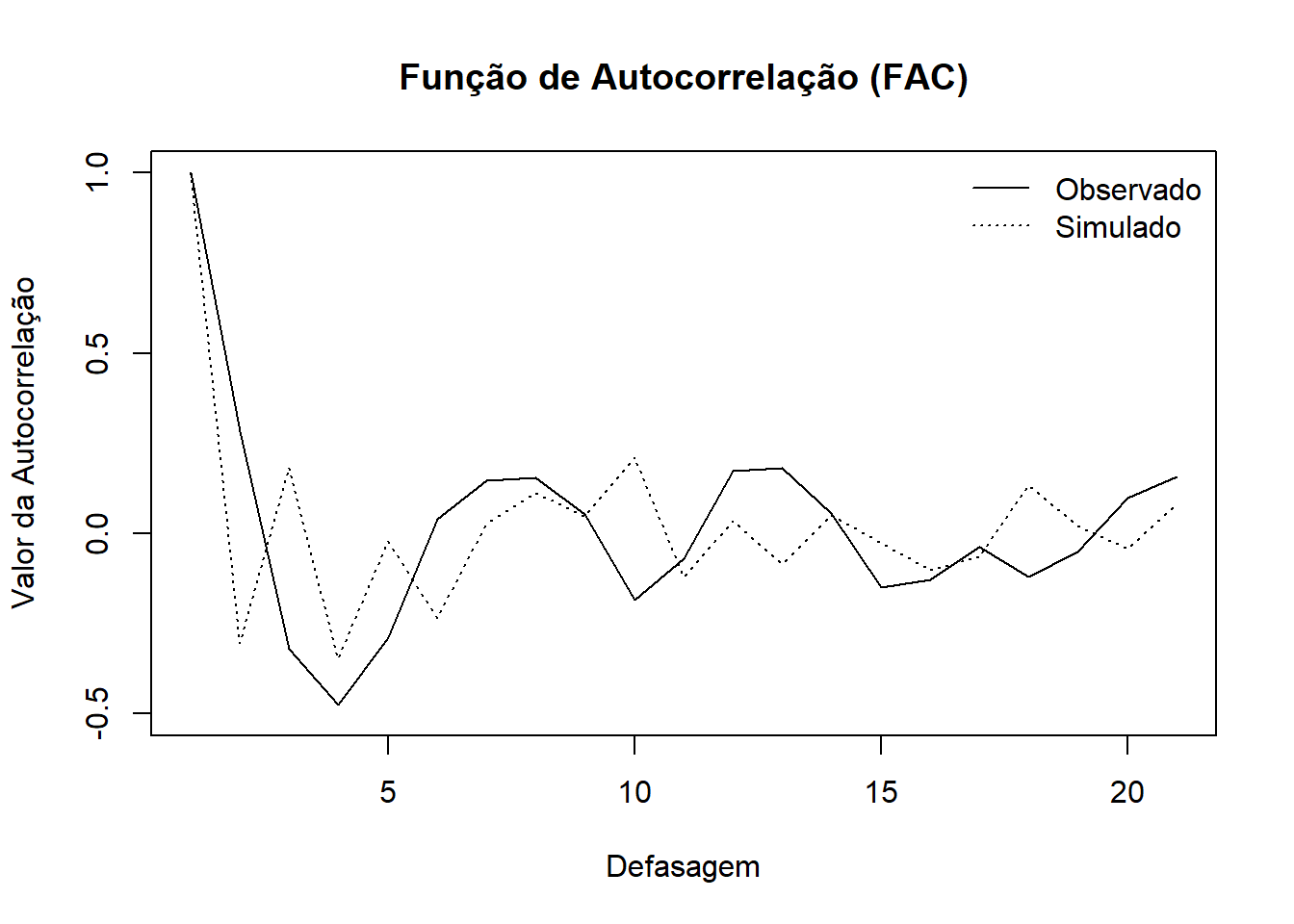
acfYactual=acf(actualY.hp$cycle, lag.max=20, plot=F)
acfY=acf(Y.hp$cycle,lag.max=20, plot=F)
plot(acfYactual$acf, ylab="Valor da Autocorrelação", xlab="Defasagem", type="l", lty=1, ylim=c(-0.5,1), main = "Função de Autocorrelação (FAC)")
lines(acfY$acf, type="l", lty=3, ylim=c(-0.5,1))
legend("topright", legend=c("Observado", "Simulado"), lty=c(1,3), bty="n")