Modelo IS-LM Dinâmico - Parte 2/2

Introdução

No post anterior, formulamos uma versão dinâmica do conhecido modelo IS-LM. Daremos continuidade avaliando outras informações do modelo. Avaliaremos aqui algumas trajetórias e o digrama de fases do modelo.

Resumidamente, temos que a dinâmica do modelo é dada por duas EDOs subsequentes: \[\dot{y}=\alpha.\left[A+a_1.y(t)-h.r(t) \right]\] \[\dot{r}=\beta.\left[-m_0+k.y(t)-u.r(t)\right] \] Em termos de script, o sistema pode ser desenhado através da seguinte função:

rm(list=ls())

IS_LM <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
  
    y <- state[1]
    r <- state[2]
    
  y_dot <- alpha*(A +a1*y -h*r) 
  r_dot <- beta*(-m0 + k*y -u*r)
  
  return(list(c(y_dot,r_dot)))
  })
}

Diferentemente do post anterior, modificamos a função em dois pontos. Deixamos apenas o sistema de derivadas que retroalimenta por integração as variáveis estado e passamos a declarar que y e r são a primeira e a segunda variaveis estado inputadas.

Na sequência, definimos como uma lista os parâmetros que serão utilizados. A lista possui a vantagem de definirmos os valores atrelados aos nomes. Como ao fim o modelo tem parâmetros agregados, utilizamos dessa primeira lista para obter os parâmetros agregados. Nesse sentido utilizamos a função attach para poder chamar na manipulação dos parâmetros agregados o nome direto da lista de parâmetros.

Parametros <- list(alpha = 0.3,
                   beta  = 0.5,
                   k     = 0.25,
                   h     = 1.3,
                   k     = 0.6,
                   u     = 0.7,
                   j     = 0.3,
                   b     = 0.7,
                   g     = 0.05,
                   q     = 0.1,
                   Tax   = 0.25,
                   M     = 30,
                   P     = 1,
                   X     = 6,
                   C_bar = 6, 
                   I_bar = 25, 
                   L_bar = 40,
                   G_bar = 15, 
                   Q_bar = 9)

attach(Parametros)

Parametros_Agregados <- list(A   = C_bar+I_bar+X+G_bar+Q_bar,
                             a1  = b*(1-Tax)+j+g-q,
                             m0  = M/P - L_bar,
                             alpha = alpha,
                             beta  = beta,
                             k     = k,
                             h     = h,
                             k     = k,
                             u     = u)

Agora, o próximo passo será através do uso do pacote phaseR. Nele, geramos o diagrama de fases através da função flowField, geramos as isóclinas (duas retas onde respectivamente \(dy/dt=0\) e \(dr/dt=0\)) através da função nullclines. Por fim, usamos a função trajectory para resolver a trajetória temporal a partir de valores iniciais do par \((y_0,r_0)\). Para solucionar algumas trajetórias, inputamos na forma de matriz os valores iniciais em 2 colunas.

library(phaseR)


IS_LM.flowField <- flowField(IS_LM, 
                             xlim = c(0,250), 
                             ylim = c(0,250),
                             parameters = Parametros_Agregados, 
                             points = 20, 
                             add = FALSE,
                             main = "Diagrama de Fase - Modelo IS-LM",
                             ylab = "Valor de r", xlab = "Valor de Y")

IS_LM.nullclines <- nullclines(IS_LM, 
                               xlim = c(0,250), 
                               ylim = c(0,250),
                               parameters = Parametros_Agregados,
                               points = 500,
                               col = c("blue","red"), 
                               lwd = 2, lty = 2,
                               add.legend = FALSE)

state <- matrix(c(10, 50, 80, 2, 50, 100), ncol = 2, nrow = 3, byrow = TRUE)

IS_LM.trajectory <- trajectory(IS_LM, 
                               y0 = state, 
                               tlim = c(0,200),
                               parameters = Parametros_Agregados, 
                               col = "black")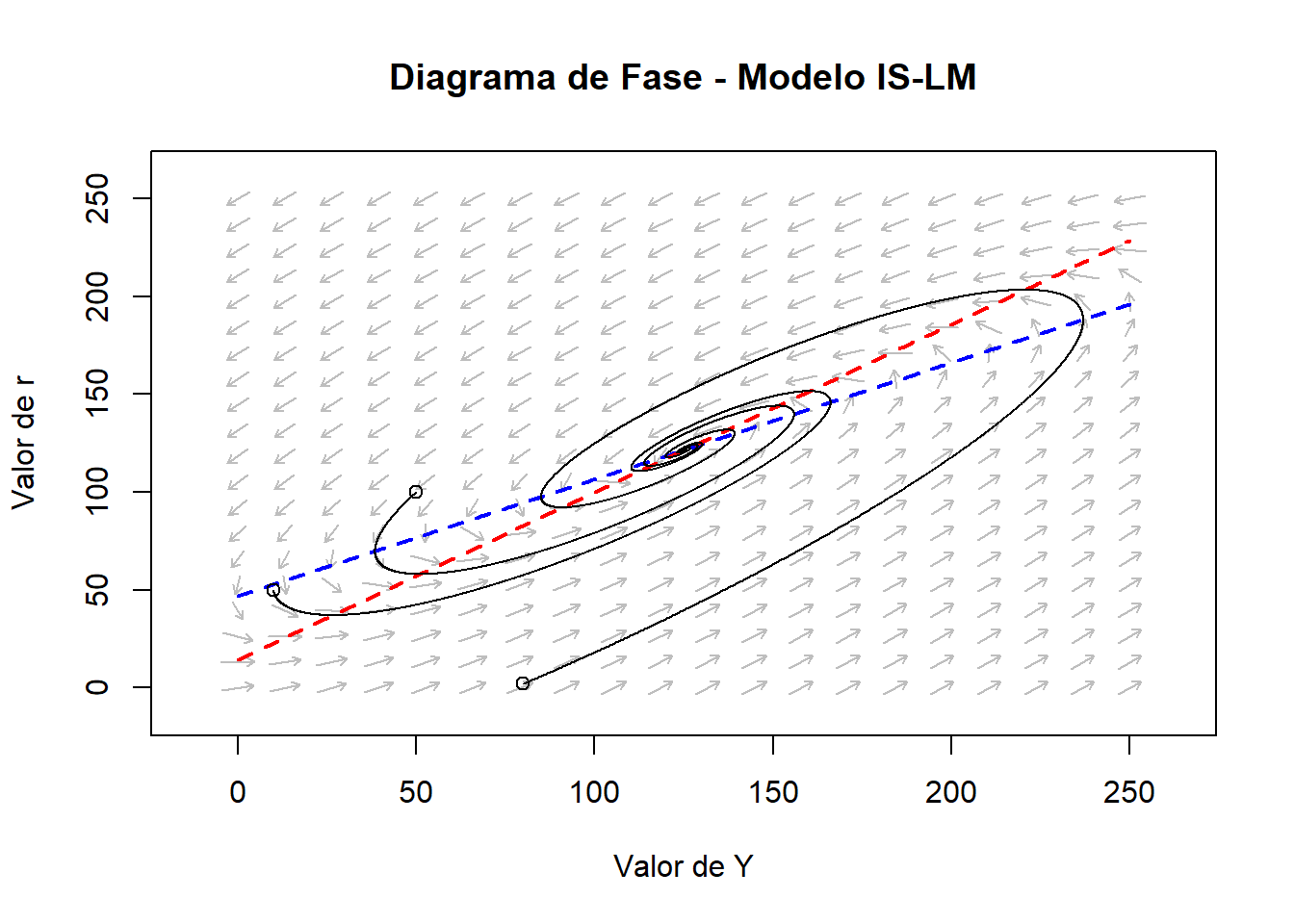

Dessa forma, concluímos esse post com o plot acima. Podemos verificar que independente do ponto de início, a trajetória do par ordenado converge para o equilíbrio. A análise de estabilidade do ponto de equilíbrio já fora verificado no post anterior. Um ponto que cabe destaque é que o ponto onde as duas isóclinas se encontram é justamente onde surge o equilíbrio, uma vez que é justamente lá que as duas derivadas são iguais a zero.