Modelo IS-LM Dinâmico - Parte 1/2

O intuito desse post é retomar um exercício feito há muito tempo atrás em um blog meu¹. A ideia original também não é minha. Na verdade, o exercício se encontra na internet realizado em rotina de Matlab pelo prof. José Maria Gaspar da Universidade do Porto². O que faremos aqui é uma certa tradução do exercício para a linguagem R, com a finalidade de explorar os pacotes de análise de dinâmica econômica.

Isso posto, vamos aqui avançar na definição matemática do modelo. Sobre a curva IS (ou Investment Saving), começamos por definir o PIB pela ótica da demanda. Assim temos que \[E(t)=C(y(t))+I(r(t),y(t))+G(y(t))+X-Q(y(t))\]

onde \(E(t)\) é a despesa ao longo do tempo; \(C(y(t))\) é o consumo agregado, como função da renda; \(I(y(t),r(t))\) é o investimento agregado como função da renda e da taxa de juros; \(G(y(t))\) representa o consumo do governo, sendo essa função da renda; \(X\) representa as exportações, sendo exógena no modelo e \(Q(y(t))\) representa as importações como função do produto.

Com relação ao mercado monetário, temos a equação que define a demanda por moeda: \[L^d(t)=\overline{L}+L(y,r)\] onde \(L^d(t)\) é a demanda por moeda, sendo essa dependente de um componente autônomo \(\overline{L}\) (preferência pela liquidez) bem como função da renda (demanda transacional) e da taxa de juros.

O modelo em versão dinâmica será conduzido pelo fechamento do hiato entre oferta e demanda no mercado de bens e serviços e a variação da taxa de juros será dada pelo fechamento do hiato entre oferta e demanda por moeda. Em termos matemáticos, temos:

\[\dot{y}=\alpha.(E-y)=\alpha.[C(y)+I(r,y)+G(y)+X-Q(y)-y]\] \[\dot{r}=\beta.(\overline{L}+L(y,r)-M/P)\] onde \(M/P\) é a oferta de moeda; \(\alpha,\beta>0\).

Sobre as variáveis, temos as seguintes definições: \[G(t)=\overline{G}+g.y(t)\] \[C(t)=\overline{C}+b.(1-T).y(t)\] \[I(t)=\overline{I}-h.r(t)+j.y(t)\] \[L^d(t)=\overline{L}+k.y(t)-u.r(t)\] \[Q(t)=\overline{Q}+q.y(t)\] onde \(h,u,\overline{C},\overline{I},\overline{L},\overline{G},\overline{Q},X>0\) e \(0<j,b,g,k,q,T<1\).

Podemos agregar os parâmetros acima de modo que os componentes autônomos da demanda sejam: \[A=\overline{C}+\overline{I}+X+\overline{G}+\overline{Q}\] Enquanto que \(m_0=M^s-\overline{L}\). A respeito da sensibilidade renda, temos a seguinte agregação: \[a_1=b.(1-T)+j-q\] Dessa forma, o sistema bidimensional de EDOs pode ser simplificado em: \[\dot{y}=\alpha.[A+a_1.y(t)-h.r(t)]\] \[\dot{r}=\beta.[-m_0+k.y(t)-u.r(t)]\] A solução de estado estacionário do sistema é dada por: \[y^*=\frac{A.u + h.m_0}{h.k-u.a_1}\] \[r^*=\frac{a_1.m_0+A.k}{h.k-u.a_1}\] A respeito da estabilidade do sistema, temos a seguinte matriz jacobiana no entorno do estado estacionário: \[J^{*}=\begin{bmatrix}\frac{\partial\dot{y}}{\partial y} & \frac{\partial\dot{y}}{\partial r}\\ \frac{\partial\dot{r}}{\partial y} & \frac{\partial\dot{r}}{\partial r} \end{bmatrix}_{y^{*},r^{*}}=\begin{bmatrix}\alpha.a_{1} & -\alpha.h\\ \beta.k & \beta.u \end{bmatrix}\] Para que o modelo apresente equilíbrio estável, devemos satisfazer pelo critério de Routh-Hurwitz: \(tr(J^*)<0\) e \(\det(J^*)>0\). Isso implica, necessariamente, em: \(a.a_1<\beta.u\) e \(k.h>a_1.u\). Portanto, se ambas são satisfeitas, o estado estacionário é estável.

Temos agora um desenho analítico mais do que suficiente para simular nosso modelo. Passemos então para o script. O primeiro passo é definir uma função que represente o sistema 2D das EDOs.

rm(list=ls())

library(deSolve) # pacote para resolver EDOs.
library(latex2exp)

Solve_IS_LM <- function(pars, times=seq(0,200,by=0.5)) {
  derivs <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
  
  y_dot <- alpha*(A +a1*y -h*r) 
  r_dot <- beta*(-m0 + k*y -u*r)
  
  return(list(c(y_dot,r_dot)))
  })
}
state <- c(y = 800, r = 0.15)
## a função ode resolve o modelo por integração.
return(ode(y = state, times = times, func = derivs, parms = pars))
}

Com relação ao conjunto de parâmetros e análise de estabilidade, temos:

# Definição dos Parâmetros
Parametros <- list(alpha = 0.3,
                   beta  = 0.5,
                   k     = 0.25,
                   h     = 1.3,
                   k     = 0.6,
                   u     = 0.7,
                   j     = 0.3,
                   b     = 0.7,
                   g     = 0.05,
                   q     = 0.1,
                   Tax   = 0.25,
                   M     = 30,
                   P     = 1,
                   X     = 6,
                   C_bar = 6, 
                   I_bar = 25, 
                   L_bar = 40,
                   G_bar = 15, 
                   Q_bar = 9)

attach(Parametros)

Parametros_Agregados <- list(A   = C_bar+I_bar+X+G_bar+Q_bar,
                             a1  = b*(1-Tax)+j+g-q,
                             m0  = M/P - L_bar,
                             alpha = alpha,
                             beta  = beta,
                             k     = k,
                             h     = h,
                             k     = k,
                             u     = u)

### Análise de Estabilidade
detach(Parametros)
attach(Parametros_Agregados)

traco        <- alpha*a1 - beta*u
determinante <- alpha*beta*(-u*a1 + k*h)
  

### Solução de Estado Estacionário
y_ast <- (A*u + h*m0)/(h*k - u*a1)
y_ast

## [1] 125.0526

r_ast <- (a1*m0 + A*k)/(h*k - u*a1)
r_ast

## [1] 121.4737

Portanto, temos no script acima a definição dos valores dos parâmetros que serão simulados e já aproveitamos a sequência para realizar o cálculo do traço e do determinante da matriz jacobiana na vizinhança do estado estacionário. Como é notório, temos atendida as condições: \(tr(J^*)<0\) e \(\det(J^*)>0\). Na sequência iremos resolver a EDO e plotar as trajetórias. Cabe aqui lembrar que resolver uma EDO é sinônimo de integrá-la. Por essa razão, criaremos uma função que oferece o cálculo das duas derivadas e essas são utilizadas para alimentar as variáveis estado. O pacote deSolve fornece a função ode()* responsável pelo método de integração numérico, o que nos permite simular as trajetórias do modelo.

## Resolução do Modelo
Out <- Solve_IS_LM(Parametros_Agregados)

## Plot do PIB x Tempo
plot(Out[,1],Out[,2], type = "l", lwd =2, col = "red",
     ylab = "PIB", xlab = "Tempo", main = "PIB x Tempo")
grid(nx = NULL, ny = NULL, col = "grey", lty = 2)
abline(h = y_ast, lty =2, lwd = 2, col = "black")
legend("topright", c("y trajetória","Estado Estacionário"),
       col = c("red","black"), lwd =2, lty = c(1,2),
       cex = 0.8, inset = 0.05)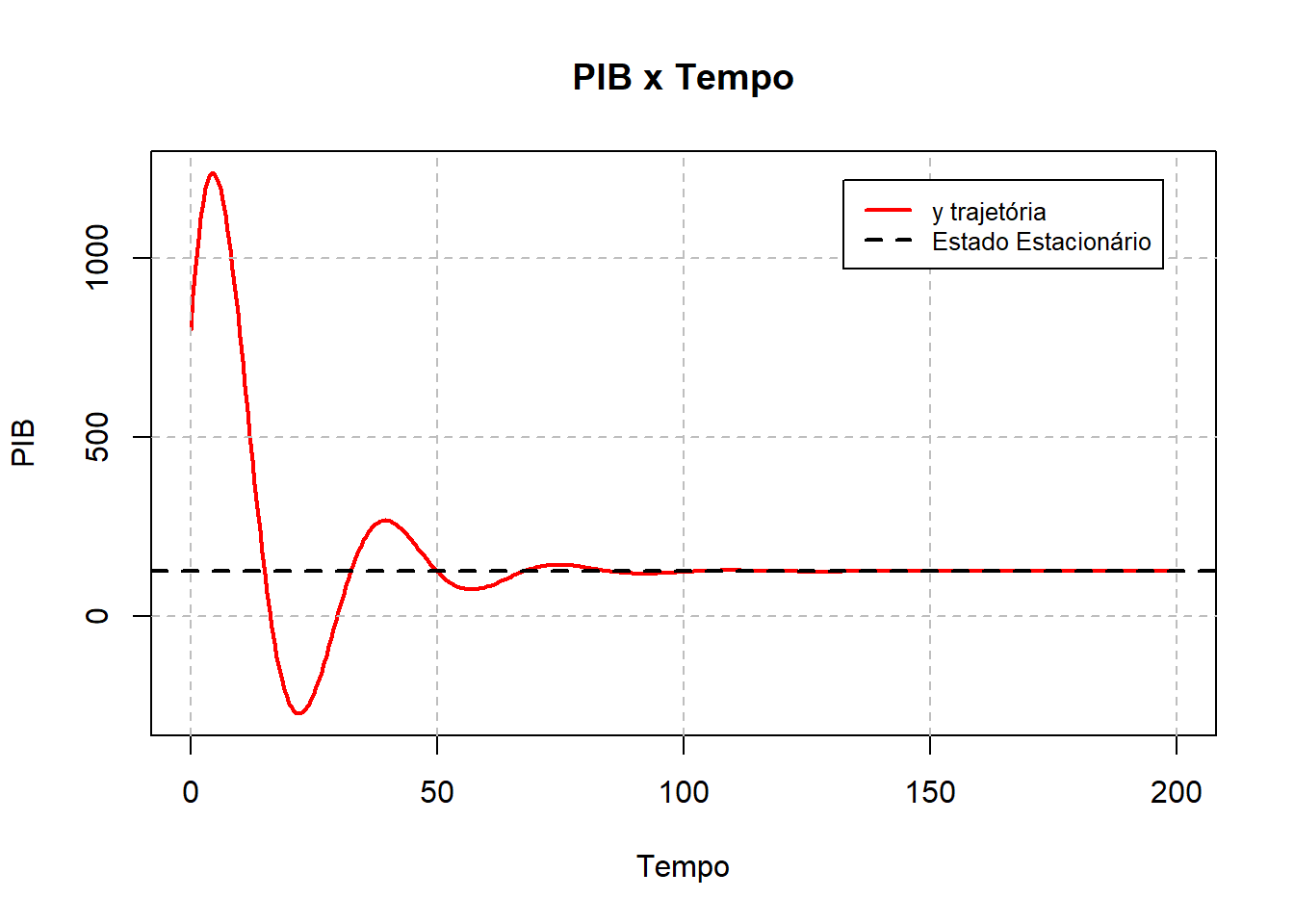

## Plot da Taxa de Juros x Tempo
plot(Out[,1],Out[,3], type = "l", lwd =2, col = "blue",
     ylab = "Taxa de Juros", xlab = "Tempo", 
     main = "Taxa de Juros x Tempo")
grid(nx = NULL, ny = NULL, col = "grey", lty = 2)
abline(h = r_ast, lty =2, lwd = 2, col = "black")
legend("topright", c("r trajetória","Estado Estacionário"),
       col = c("blue","black"), lwd =2, lty = c(1,2),
       cex = 0.8, inset = 0.05)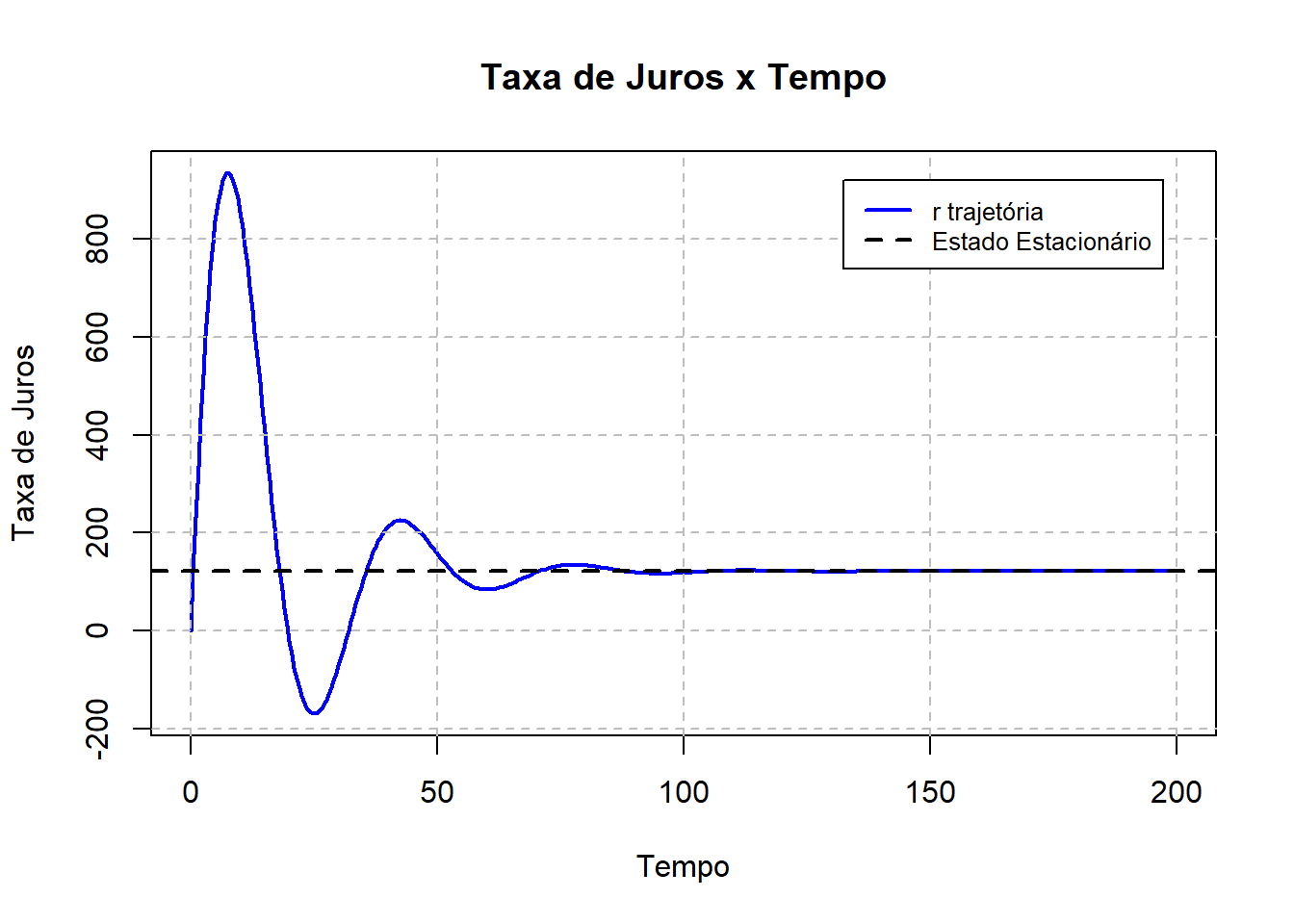

## Plot do Retrato de Fase
plot(Out[,2],Out[,3], type = "l", lwd =2, col = "magenta",
     ylab = "Taxa de Juros", xlab = "PIB", 
     main = "Retrato de Fase - PIB x Taxa de Juros")
grid(nx = NULL, ny = NULL, col = "grey", lty = 2)
abline(h = y_ast, lty =2, lwd = 2, col = "grey")
abline(v = r_ast, lty =2, lwd = 2, col = "green")
legend("bottomright",c(TeX("$(r,y)$ - trajetória"),TeX("$r^*$"),TeX("$y^*$")),
       cex = 0.8, inset = 0.05, lwd =2, lty = c(1,2,2),
       col = c("magenta","grey","green"))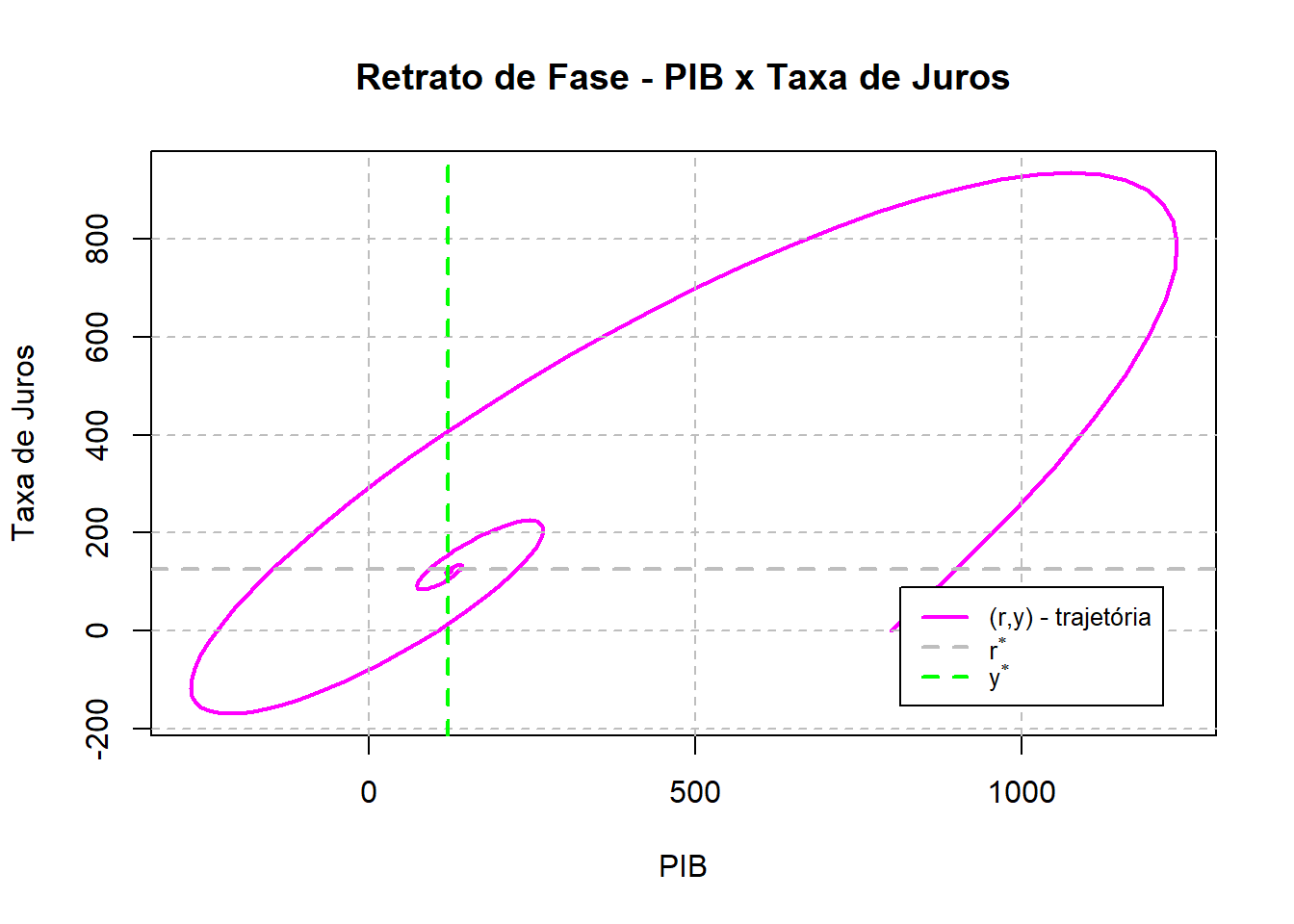

Podemos então verificar pelas simulações realizadas que a trajetória converge e se estabiliza em torno da solução de estado estacionário. No próximo post iremos explorar outras propriedades e análises do modelo.