Metodologia ARDL (Cookbook) e Curva de Phillips Híbrida no Brasil
O intuito geral desse post é apresentar a aplicação (na forma de receita de bolo) do método de estimação ARDL no R, com um exemplo aplicado para a inflação brasileira. Para iniciar, explicaremos a parte teórica do ARDL.
Estimação do ARDL (Discussão Teórica)
Seguem aqui alguns passos resumidos de como iremos estimar o modelo por ARDL (Autoregressive Distributed Lag):
Sua forma básica (exemplo para para duas variáveis): \[y_t=\beta_0+\beta_1.y_{t-1}+\ldots+\beta_p.y_{t-p}+\alpha_0.x_t+\alpha_1.x_{t-1}+\ldots+\alpha_q.x_{t-q}+\epsilon_t\;\;\;(1)\]
onde \(\beta_{i},\;i \in [1,\ldots,p]\) são os parâmetros que capturam o efeito autoregressivo da variável endógena; \(\alpha_i,\;\in[1,\ldots,q]\) são os parâmetros que capturam o efeito contemporâneo e defasado da variável explicativa; \(\epsilon_t\) é o termo de erro na forma de ruído branco.
- Certificar que nenhuma das variáveis é \(I(2)\). Caso contrário, os dados invalidam a metodologia.
- Formular um modelo “irrestrito” de correções de erros (MCE). Esse é um tipo particular de modelo ARDL.
- Determinar a estrutura apropriada das defasagens para o modelo referido no passo 2.
- Certificar que os erros do modelo são serialmente independentes.
- Certificar que o modelo é “dinamicamente estável”.
- Rodar o teste de limites para verificar se há evidência de relação de longo prazo entre as variáveis.
- Se o resultado do passo anterior for positivo, estimar um modelo de longo prazo em nível, bem como um MCE restrito.
- Usar os resultados da estimação do passo 7 para medir os efeitos dinâmicos de curto prazo e as relação de equilíbrio de longo prazo entre as variáveis.
Antes de seguir adiante, vamos relembrar a forma que o MCE para dados cointegrados possui (exemplo para 1 variável endógena e 2 explicativas): \[\Delta y_t=\beta_0+\sum_1^{p}\beta_i.\Delta y_{t-i}+\sum_0^{q_1}\gamma_j.\Delta x_{1(t-j)}+\sum_0^{q_2}\delta_k.\Delta x_{2(t-k)}+\phi.z_{t-1}+e_t\;\;\;(2)\] onde \(z\), o termo de correção de erro, é o resíduo por MQO da regressão cointegrada de longo prazo, dada por: \[y_t=\alpha_0+\alpha_1.x_{1t}+\alpha_2.x_{2t}+v_t\;\;\;(3)\]
E agora, podemos expandir o roteiro acima para maiores detalhes:
1º Passo: Usar testes de raízes unitárias para verificar se não estamos lidando com séries \(I(2)\). Para esse fim, podemos fazer uso do ADF, PP, KPSS, entre outros testes.
2º Passo: Formular o seguinte modelo: \[\Delta y_t=\beta_0+\sum_1^p\beta_i.\Delta y_{t-i}+\sum_0^{q_1}\gamma_j.\Delta x_{1(t-j)}+\sum_0^{q_2}\delta_k.\Delta x_{2(t-k)}+\] \[\theta_0.y_{t-1}+\theta_1.x_{1(t-1)}+\theta_2.x_{2(t-1)}+e_t\;\;\;(4) \]
Repare que a especificação é quase a mesma de um MCE tradicional. Uma diferença é que nós trocamos o termo de correção de erros, \(z_{t-1}\), com os termos \(y_{t-1},x_{1(t-1)},x_{2(t-1)}\). Da equação de longo prazo, podemos ver que \(z_{t-1}=y_{t-1}-a_0-a_1.x_{1(t-1)}-a_2.x_{2(t-1)}\), onde os parâmetros “\(a's\)” são estimações por MQO para os \(\alpha's\). Então, o que fazemos na equação anterior é incluir os mesmos níveis defasados como nós fazemos no MCE regular, mas não vamos restringir esses coeficientes. Inclusive, esse é o motivo de chamarmos MCE irrestrito. Na nomenclatura de Pesaran et al. (2001) ele é chamado de MCE condicional.
3º Passo: A amplitude do somatório na equação acima são, respectivamente, de \([1,p];[0,q_1];[0,q_2]\). Nós devemos selecionar ,os valores apropriados para as defasagens máximas, \(p,q_1,q_2\). Também, repare que pode não ser necessária defasagem zero em \(\Delta x_1\) e \(\Delta x_2\). Usualmente, a máxima defasagem é determinada utilizando o critério de informação, tal como AIC, SC (BIC), HQ, etc. Esses critérios são baseados em um alto valor para log-verossimilhança, penalizando a escolha de incluir mais lags para esse fim. A forma da penalidade varia de um critério para o outro. Cada critério começa com \(-2.\log(L)\) e então penaliza, de modo que o menor valor do critério da informação é o melhor resultado encontrado.
4º Passo Uma premissa chave no ARDL/Teste de Limites da metodologia de Pesaran et al. (2001) é que os erros da equação deve ser serialmente independentes. Como os autores reparam (p. 308), este requisito pode também influenciar na nossa escolha final do máximo de lags das variáveis do modelo.
Portanto, uma vez que uma versão plausível do modelo tenha sido estimada, nós devemos fazer uso do teste LM para testar a hipótese nula, na qual os erros são serialmente independentes, contra a hipótese alternativa que os erros são (tanto) \(AR(m)\) ou \(MA(m)\), para \(m=1,2,3,\ldots\).
5º Passo Nós temos um modelo com uma estrutura autoregressiva, então nós devemos certificar que o modelo é “Dinamicamente Estável”. O que precisamos fazer então é verificar que todas as raízes inversas da equação característica associada ao modelo ficam estritamente dentro do círculo unitário.
6º Passo Agora vamos realizar o teste de de Limites da Metodologia de Pesaran et al. (2001): Novamente, trazemos a equação \((4)\):
\[\Delta y_t=\beta_0+\sum_1^p\beta_i.\Delta y_{t-i}+\sum_0^{q_1}\gamma_j.\Delta x_{1(t-j)}+\sum_0^{q_2}\delta_k.\Delta x_{2(t-k)}+\] \[\theta_0.y_{t-1}+\theta_1.x_{1(t-1)}+\theta_2.x_{2(t-1)}+e_t\] O que precisamos fazer é rodar um teste-F para a hipótese nula \(H_0:\;\theta_1=\theta_2=0\). A hipótese alternativa é \(H_1:\;\theta_1\;e/ou\;\theta_2\neq0\). Parece bastante simples, mas por que fazemos esse teste?
Como em um teste convencional de cointegração, nós estamos testando para a ausência de uma relação de equilíbrio de longo prazo entre as variáveis. Essa ausência coincide com obter coeficientes zero para \(y_{t-1},x_{1(t-1)},x_{2(t-1)}\) na equação \((4)\). A rejeição de \(H_0\) implica no aceite de uma relação de longo prazo.
Todavia, há uma dificuldade prática que deve ser endereçada quando realizado o teste-F. A distribuição do teste é totalmente não padronizada (e também depende de um “parâmetro de perturbação”, o posto de cointegração do sistema) mesmo no caso assintótico onde nós temos um tamanho de amostra infinitamente grande. (Isso de alguma forma se assemelha a situação que ocorre com o teste Wald quando testamos para a causalidade de Granger na presença de dados não estacionários. Neste caso, o problema é contornado usando o procedimento de Toda-Yanamoto (1995) para garantir que a estatística do teste de Wald seja assintoticamente igual \(\chi^2\)).
Os valores críticos exatos para o teste-F não estão disponíveis para uma mistura arbitrária de variáveis \(I(0)\) e \(I(1)\). Todavia, Pesaran et al. (2001) oferecem limites para os valores críticos para a distribuição assintótica da estatística-F. Para várias situações (isto é, números diferentes de variáveis, \((k+1)\)), os autores fornecem os limites inferiores e superiores para os valores críticos. Em cada caso, o valor inferior é baseado na premissa que todas as variáveis são \(I(0)\) e o limite superior é baseado na premissa que todas as variáveis sejam \(I(1)\). Na verdade, qualquer mix desejado estará entre esses limites extremos.
Se o valor calculado da estatística-F estiver abaixo do limite inferior, podemos concluir que as variáveis são \(I(0)\), então, por definição não é possível ter cointegração. Se a estatística-F calculada estiver acima do limite superior, podemos concluir que há cointegração. Por fim, se o valor calculado estiver entre os limites inferior e superior, o resultado do teste é inconclusivo.
Como uma forma de confirmação, podemos rodar um “Teste-t limite” com \(H_0:\theta_0=0\) e \(H_1:\theta_0<0\). Se a estatística-t para \(y_{t-1}\) na equação (4) for maior que o limite de \(I(1)\) tabulado por Pesaran et al. (2001, p. 303-304), isso dá suporte para a conclusão que há uma relação de longo prazo entre as variáveis. Se a estatística-t é menor que o limite para \(I(0)\), nós devemos concluir que os dados são todos estacionários.
7º Passo Assumindo que o teste nos leve a conclusão de cointegração, nós podemos estimar a relação de longo prazo entre as variáveis, dada pela equação (3):
\[y_t=\alpha_0+\alpha_1.x_{1t}+\alpha_2.x_{2t}+v_t\] Bem como o MCE, dado pela equação (2): \[\Delta y_t=\beta_0+\sum_1^{p}\beta_i.\Delta y_{t-i}+\sum_0^{q_1}\gamma_j.\Delta x_{1(t-j)}+\sum_0^{q_2}\delta_k.\Delta x_{2(t-k)}+\phi.z_{t-1}+e_t\] onde \(z_{t-1}=y_{t-1}-a_0-a_1.x_{1(t-1)}-a_2.x_{2(t-1)}\) e os \(a's\) são estimações de \(\alpha's\) apresentados na equação (3).
8º Passo Nós podemos extrair os efeitos de longo prazo do modelo MCE irrestrito. Olhando a equação (4) e reparando que no equilíbrio de longo prazo \(\Delta y_t=\Delta x_{1(t)}=\Delta x_{2(t)}=0\), temos por decorrência disso que os coeficientes de longo prazo para \(x_1\) e \(x_2\) são \(-\theta_1/\theta_0\) e \(-\theta_2/\theta_0\), respectivamente.
Exemplo Aplicado - Estimação da Curva Híbrida de Phillips para a Economia Brasileira
1ª Parte - Obtenção e Tratamento dos Dados Nesta seção iremos obter as séries de dados e tratá-las para sazonalidade, além de compor a inflação mensal para a janela anual composta de 12 meses.
Séries que serão utilizadas do Ipeadata:
- Inflação Mensal - IPCA Geral a.m. - A Taxa será acumulada para 12 meses (cod.: PRECOS12_IPCAG12)
- Expectativa Média de Inflação - IPCA - Taxa Acumulada para os próximos 12 meses (cod.: BM12_IPCAEXP1212)
- Índice de Atividade Econômica do Banco Central (IBC-Br) - Índice Utilizado para o cálculo do Hiato do Produto (Cod.: SGS12_IBCBR12)
- Taxa de Câmbio Real Efetiva - INPC - Importações (Cod.: GAC12_TCERMTINPC12)
library(ipeadatar)
# Séries via data.frame
IPCA_m_df <- ipeadata(code = "PRECOS12_IPCAG12")
Exp_Inf_df <- ipeadata(code = "BM12_IPCAEXP1212")
IBC_BR_df <- ipeadata(code = "SGS12_IBCBR12")
TCRE_Imp_df <- ipeadata(code = "GAC12_TCERMTINPC12")
# Transformando de data.frame para time.series
IPCA_ts <- ts(IPCA_m_df$value*0.01, start = c(1980,01), frequency = 12)
Exp_Inf_ts <- ts(Exp_Inf_df$value*0.01, start = c(2001,07), frequency = 12)
IBC_BR_ts <- ts(IBC_BR_df$value, start = c(2003,01), frequency = 12)
TCRE_ts <- ts(TCRE_Imp_df$value, start = c(1982,01), frequency = 12)
par(mfrow = c(2,2))
plot(IPCA_ts,
main = "Taxa de Inflação Mensal - IPCA",
col = "magenta",
lwd = 2,
ylab = "Inflação Mensal",
xlab = "Tempo (Meses)")
plot(Exp_Inf_ts,
main = "Expectativa Média de Inflação (12 Meses)",
col = "red",
lwd = 2,
ylab = "Inflação Esperada",
xlab = "Tempo (Meses)")
plot(IBC_BR_ts,
main = "IBC-BR - Índice de Atividade Econômica",
col = "dark green",
lwd = 2,
ylab = "Número-Índice",
xlab = "Tempo (Meses)")
plot(TCRE_ts,
main = "Taxa de Câmbio Real Efetiva - Imp.",
col = "blue",
lwd = 2,
ylab = "Número-Índice",
xlab = "Tempo (Meses)")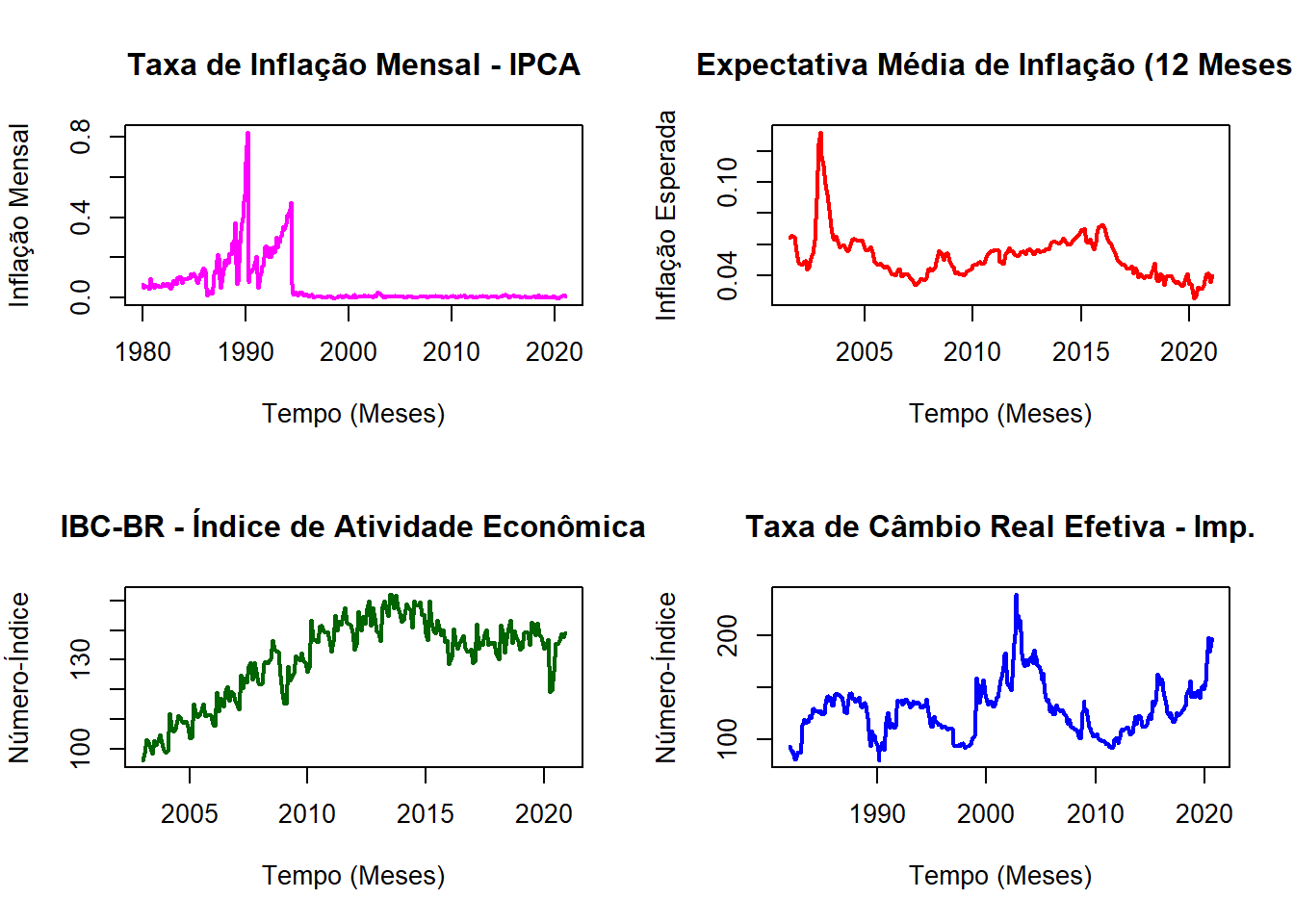
Das figuras geradas para as 4 séries temos: (a) A necessidade de acumular a inflação para 12 meses e selecionar o período pós plano real (devido ao efeito de hiperinflação da série); (b) Sobre a expectativa, nada precisa ser feito; (c) Dessazonalizar o IBC-BR e posteriormente calcular o hiato do produto utilizando o filtro HP e posteriormente aplicar o log; (d) verificar se há carga sazonal e posteriormente aplicar o log. Portanto, faremos isso agora!
library(seasonal)
# Recorte do IPCA pós Plano Real
IPCA_pos_95 <- window(IPCA_ts, start = c(1995,1))
IPCA_12 <-(((1+IPCA_pos_95)*(1+stats::lag(IPCA_pos_95,-1))*
(1+stats::lag(IPCA_pos_95,-2))*
(1+stats::lag(IPCA_pos_95,-3))*
(1+stats::lag(IPCA_pos_95,-4))*
(1+stats::lag(IPCA_pos_95,-5))*
(1+stats::lag(IPCA_pos_95,-6))*
(1+stats::lag(IPCA_pos_95,-7))*
(1+stats::lag(IPCA_pos_95,-8))*
(1+stats::lag(IPCA_pos_95,-9))*
(1+stats::lag(IPCA_pos_95,-10))*
(1+stats::lag(IPCA_pos_95,-11)))-1)
plot(IPCA_12, col = "brown", main = "IPCA Acumulado em 12 Meses", lwd = 2,
ylab = "Inflação Acumulada (valor decimal)",
xlab = "Tempo (meses)")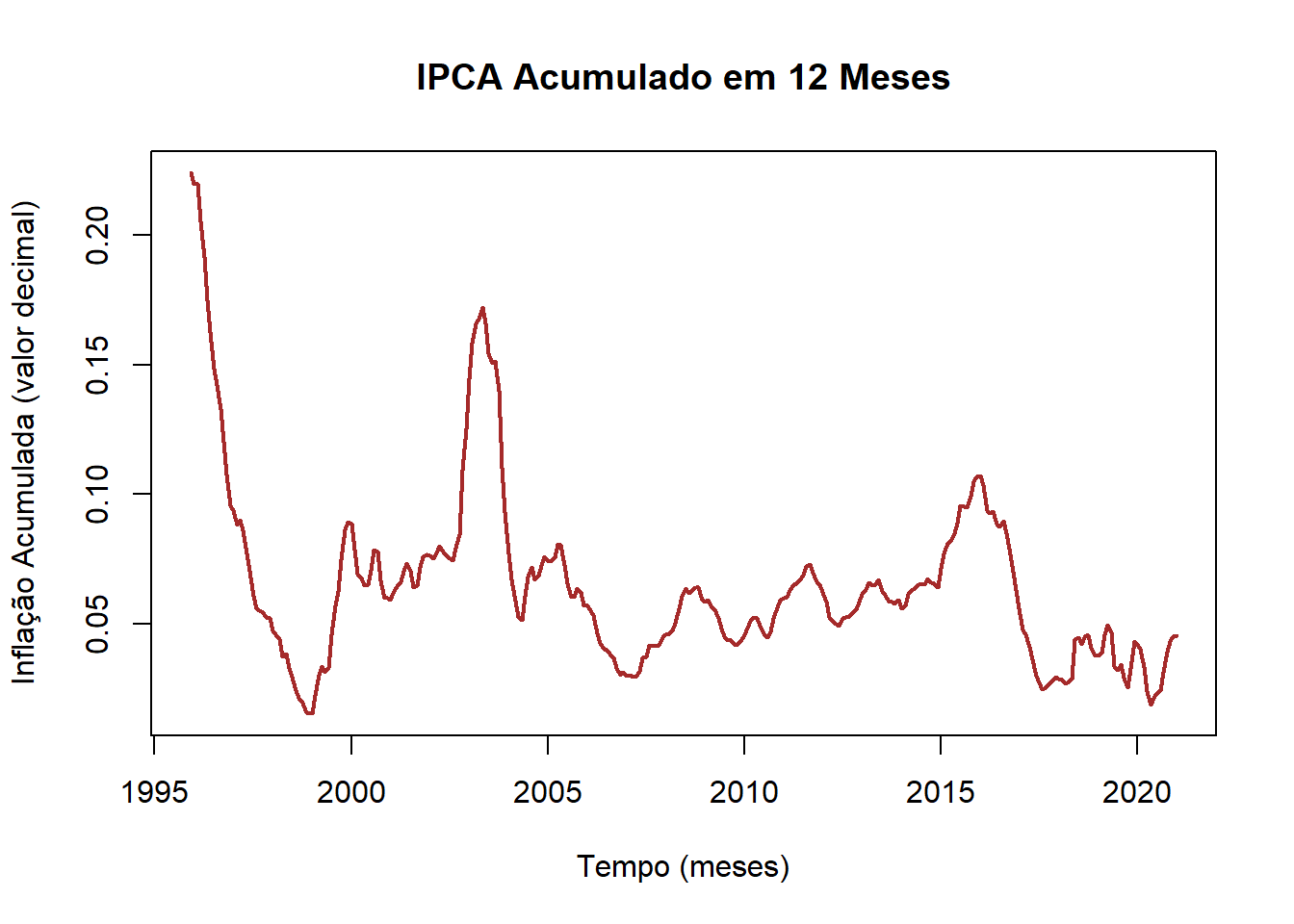
# Tratamento de Sazonalidade
Seas_IBC_BR <- seas(IBC_BR_ts)
# Armazenamento em uma ts.
IBC_BR_seas <- Seas_IBC_BR$data[,3]
plot(Seas_IBC_BR, main = "Série Original e Ajustada para Sazonalidade no IBC-BR")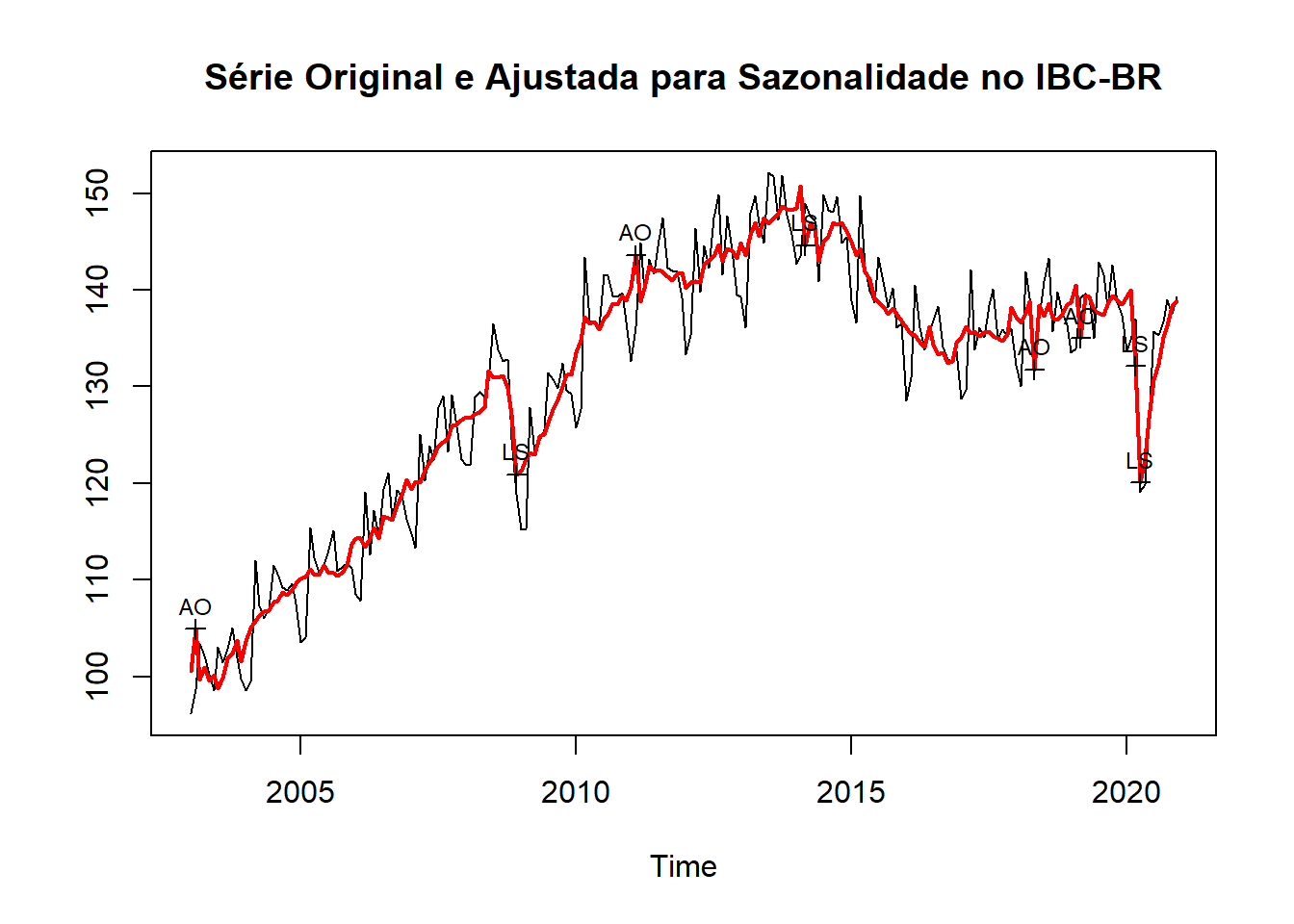
library(mFilter)
# Cálculo do Hiato do Produto
IBC.hp <- hpfilter(IBC_BR_seas)
Hiato <- IBC_BR_seas/IBC.hp$trend -1
plot(Hiato, main = "Hiato do Produto - Filtro HP",
ylab = "Hiato %", xlab = "Tempo")
abline(h = 0, lty = 2, lwd = 2, col = "red")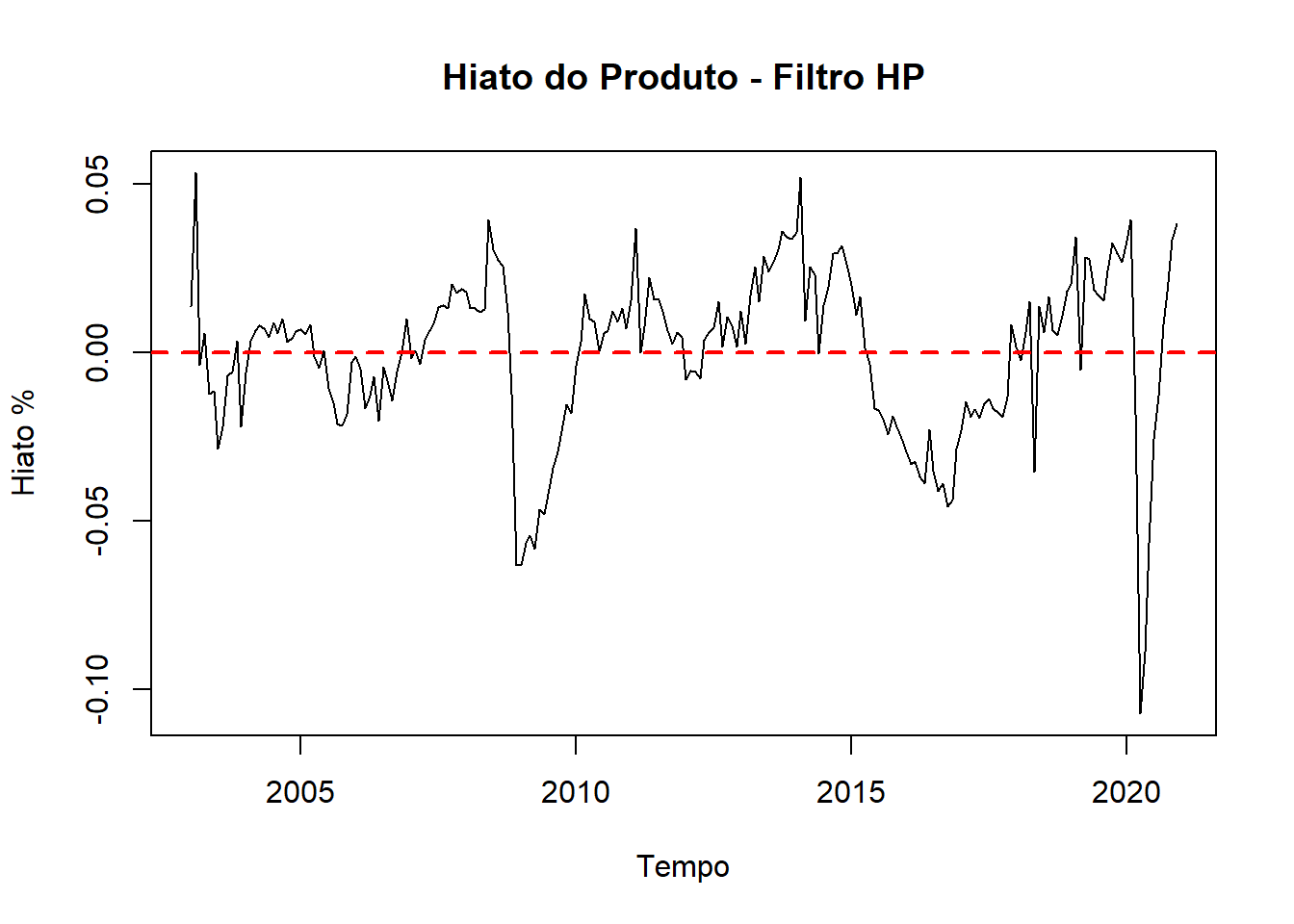
Tendo obtido o Hiato do Produto, a taxa de Câmbio Real Efetiva das Importações e a Inflação Acumulada em 12 meses, vamos juntar lado a lado os dados e recortar a janela temporal para igual início e fim. A janela comum a todas as séries é janeiro de 2003 (data de início da série do IBC-BR) até setembro de 2020 que é a última observação mensal da Taxa de Câmbio Real Efetiva.
Dados <- window(cbind(IPCA_12,Hiato,Exp_Inf_ts,TCRE_ts),
start = c(2003,1),
end = c(2020,9))
colnames(Dados) <- c("IPCA","Hiato","Expectativa","TCRE")
tail(Dados)## IPCA Hiato Expectativa TCRE
## [208,] 0.02399045 -0.107314677 0.0250 186.2241
## [209,] 0.01877488 -0.089082491 0.0267 197.8883
## [210,] 0.02132156 -0.056510910 0.0322 184.4718
## [211,] 0.02305451 -0.025638874 0.0320 188.3577
## [212,] 0.02438302 -0.012949466 0.0314 197.3506
## [213,] 0.03135162 0.008372225 0.0337 194.78762ª Parte - Etapas do ARDL
Vamos começar fazendo os testes de raíz unitária para certificar que não haja variáveis \(I(2)\).
library(urca)
library(fUnitRoots)
library(kableExtra)
# Teste ADF para as Variáveis em Nível
unitRoot_IPCA = adfTest(Dados[,1],lags=3, type=c("c"))
unitRoot_Hiato = adfTest(Dados[,2],lags=3, type=c("c"))
unitRoot_Expec = adfTest(Dados[,3],lags=3, type=c("c"))
unitRoot_TCRE = adfTest(Dados[,4],lags=3, type=c("c"))
# Tabela com os resultados do teste
adf_IPCA = c(unitRoot_IPCA@test$statistic, unitRoot_IPCA@test$p.value)
adf_Hiato = c(unitRoot_Hiato@test$statistic, unitRoot_Hiato@test$p.value)
adf_Expec = c(unitRoot_Expec@test$statistic, unitRoot_Expec@test$p.value)
adf_TCRE = c(unitRoot_TCRE@test$statistic, unitRoot_TCRE@test$p.value)
resultADF = cbind(adf_IPCA, adf_Hiato, adf_Expec, adf_TCRE)
colnames(resultADF) = c("IPCA 12 Meses", "Hiato do Produto", "Expectativa de Inflação", "TCRE das Importações")
rownames(resultADF) = c("Estatística do Teste ADF - Nível", "p-valor")
kable(round(resultADF, digits = 4)) %>%
kable_styling(bootstrap_options = c("striped","hover"))| IPCA 12 Meses | Hiato do Produto | Expectativa de Inflação | TCRE das Importações | |
|---|---|---|---|---|
| Estatística do Teste ADF - Nível | -4.7398 | -4.1942 | -3.5127 | -1.2672 |
| p-valor | 0.0100 | 0.0100 | 0.0100 | 0.5851 |
# Teste do ADF para a 1ª Diferença
unitRoot_IPCA = adfTest(diff(Dados[,1]),lags=3, type=c("c"))
unitRoot_Hiato = adfTest(diff(Dados[,2]),lags=3, type=c("c"))
unitRoot_Expec = adfTest(diff(Dados[,3]),lags=3, type=c("c"))
unitRoot_TCRE = adfTest(diff(Dados[,4]),lags=3, type=c("c"))
# Tabela com os resultados do teste
adf_IPCA = c(unitRoot_IPCA@test$statistic, unitRoot_IPCA@test$p.value)
adf_Hiato = c(unitRoot_Hiato@test$statistic, unitRoot_Hiato@test$p.value)
adf_Expec = c(unitRoot_Expec@test$statistic, unitRoot_Expec@test$p.value)
adf_TCRE = c(unitRoot_TCRE@test$statistic, unitRoot_TCRE@test$p.value)
resultADF = cbind(adf_IPCA, adf_Hiato, adf_Expec, adf_TCRE)
colnames(resultADF) = c("IPCA 12 Meses",
"Hiato do Produto",
"Expectativa de Inflação",
"TCRE das Importações")
rownames(resultADF) = c("Estatística do Teste ADF - Diff", "p-valor")
kable(round(resultADF, digits = 4)) %>%
kable_styling(bootstrap_options = c("striped","hover"))| IPCA 12 Meses | Hiato do Produto | Expectativa de Inflação | TCRE das Importações | |
|---|---|---|---|---|
| Estatística do Teste ADF - Diff | -5.2162 | -8.1217 | -6.7925 | -6.9721 |
| p-valor | 0.0100 | 0.0100 | 0.0100 | 0.0100 |
Estimação do Modelo
Na sequência, testamos o melhor modelo ARDL utilizando o critério de informação de AIC. O melhor modelo encontrado foi com as seguintes ordens \(2,0,1,1\). Depois especificamos esse modelo e realizamos o teste-F para um modelo com constante irrestrita. Podemos verificar pelo report que rejeitamos a hipótese nula, portanto, aceitando que haja cointegração entre as variáveis. Vale lembrar que havíamos previamente identificado que todas as variáveis são \(I(0)\) e apenas a TCRE é \(I(1)\).
Na sequência, através do pacote dLagM, podemos rodar o teste de limites e obter alguns diagnósticos do modelo para a estimação de ARDL. A função ardlBound() nos permite procurar via critério da informação (podendo escolher se usa AIC, BIC, etc) qual a defasagem adequada para o modelo.
Feito isso, temos a escolha do melhor lag como sendo \((2,1,1,1)\), pelo critério de \(AIC\).
A respeito dos resíduos, realiza-se o teste de Breusch-Godfrey para verificar se há autocorrelação. Como resultado, aceitamos a \(H_0\) de que não haja autocorrelação. Um segundo teste para verificar autocorrelação realizado é o Box-Ljung. O resultado também confirma a ausência de autocorrelação.
Além da autocorrelação, verificamos a homocedasticidade dos resíduos bem como a normalidade. Como é desejável um comportamento estilo ruído branco, espera-se encontrar através do teste Breusch-Pagan a aceitação da hipótese alternativa, confirmando a homocedasticidade. Com relação a normalidade, realiza-se o teste Shapiro-Wilk. O esperado também é encontrar o aceite da hipótese alternativa, concluindo pela normalidade. Cabe destacar que esses foram os resultados obtidos.
Com relação ao teste dos limites para verificar se há cointegração, obtivemos como resultado a estatística-F de \(7.5525\) e esse valor é acima do limite superior para 10%, 5% e 1% de valores críticos. Portanto, podemos aceitar que tenhamos uma relação de longo prazo entre as variáveis.
Pelo teste de RESET, podemos verificar se a especificação do modelo foi feita correta.
A respeito da estabilidade do modelo, a inspeção visual do CUSUM Recursivo dos Resíduos, CUSUM Recursivo dos Quadrados dos Resíduos e do Recursivo MOSUM nos leva a concluir que o modelo é estável.
library(dLagM)
library(permutations)
Dadosdf <- data.frame(Dados)
Report_ARDL <- ardlBound(data = Dadosdf,
formula = IPCA ~ Hiato + Expectativa + TCRE,
ic = "AIC", max.p = 6, max.q = 6, ECM = TRUE,
stability = TRUE)##
## Orders being calculated with max.p = 6 and max.q = 6 ...
##
## Autoregressive order: 2 and p-orders: 1 1 1
## ------------------------------------------------------
##
## Breusch-Godfrey Test for the autocorrelation in residuals:
##
## Breusch-Godfrey test for serial correlation of order up to 1
##
## data: modelFull$model
## LM test = 0.045607, df1 = 1, df2 = 201, p-value = 0.8311
##
## ------------------------------------------------------
##
## Ljung-Box Test for the autocorrelation in residuals:
##
## Box-Ljung test
##
## data: res
## X-squared = 0.020871, df = 1, p-value = 0.8851
##
## ------------------------------------------------------
##
## Breusch-Pagan Test for the homoskedasticity of residuals:
##
## studentized Breusch-Pagan test
##
## data: modelFull$model
## BP = 38.743, df = 8, p-value = 5.486e-06
##
## The p-value of Breusch-Pagan test for the homoskedasticity of residuals: 5.485989e-06 < 0.05!
## ------------------------------------------------------
##
## Shapiro-Wilk test of normality of residuals:
##
## Shapiro-Wilk normality test
##
## data: modelFull$model$residual
## W = 0.94107, p-value = 1.506e-07
##
## The p-value of Shapiro-Wilk test normality of residuals: 1.506388e-07 < 0.05!
## ------------------------------------------------------
##
## PESARAN, SHIN AND SMITH (2001) COINTEGRATION TEST
##
## Observations: 212
## Number of Regressors (k): 3
## Case: 3
##
## ------------------------------------------------------
## - F-test -
## ------------------------------------------------------
## <------- I(0) ------------ I(1) ----->
## 10% critical value 2.72 3.77
## 5% critical value 3.23 4.35
## 1% critical value 4.29 5.61
##
##
## F-statistic = 7.55255119933262
##
## ------------------------------------------------------
## F-statistic note: Asymptotic critical values used.
##
## ------------------------------------------------------
##
## Ramsey's RESET Test for model specification:
##
## RESET test
##
## data: modelECM$model
## RESET = 0.24805, df1 = 2, df2 = 203, p-value = 0.7806
##
## ------------------------------------------------------## ------------------------------------------------------
## Error Correction Model Output:
##
## Time series regression with "ts" data:
## Start = 2, End = 212
##
## Call:
## dynlm(formula = as.formula(model.text), data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.0160297 -0.0017477 0.0000308 0.0015301 0.0109303
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.136e-03 1.132e-03 -5.419 1.67e-07 ***
## ec.1 -8.437e-02 1.524e-02 -5.537 9.35e-08 ***
## dHiato.t -1.599e-02 1.542e-02 -1.037 0.301
## dExpectativa.t 6.667e-01 7.724e-02 8.632 1.69e-15 ***
## dTCRE.t -6.493e-05 4.584e-05 -1.416 0.158
## dIPCA.1 5.886e-01 4.624e-02 12.730 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.00309 on 205 degrees of freedom
## Multiple R-squared: 0.5921, Adjusted R-squared: 0.5821
## F-statistic: 59.5 on 5 and 205 DF, p-value: < 2.2e-16
##
## ------------------------------------------------------
## Long-run coefficients:
## IPCA.1 Hiato.1 Expectativa.1 TCRE.1
## -8.437346e-02 -1.309134e-02 1.742597e-01 1.747854e-05
## Report_ARDL$p## IPCA Hiato Expectativa TCRE
## 1 2 1 1 1Referências
Pesaran, M. H. and Y. Shin, 1999. An autoregressive distributed lag modelling approach to cointegration analysis. Chapter 11 in S. Strom (ed.), Econometrics and Economic Theory in the 20th Century: The Ragnar Frisch Centennial Symposium. Cambridge University Press, Cambridge. (Discussion Paper version.)
Pesaran, M. H., Shin, Y. and Smith, R. J., 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics, 16, 289–326.
Pesaran, M. H. and R. P. Smith, 1998. Structural analysis of cointegrating VARs. Journal of Economic Surveys, 12, 471-505.
Toda, H. Y and T. Yamamoto (1995). Statistical inferences in vector autoregressions with possibly integrated processes. Journal of Econometrics, 66, 225-250.