Medidas de Risco e Volatilidade - Índice Ibovespa
Introdução e Problema
Os veículos de comunicação têm noticiado durante o ano de 2020 fortes quedas na bolsa de valores do mundo todo e em particular da B3. Em virtude disso, torna-se importante investigarmos com maior detalhes que informações podemos obter desse movimento. Qual é a volatilidade no período? Ela é a maior já experimentada na série histórica? Qual o tempo médio de recuperação em movimentos similares a esse? Nesse sentido, faremos uso das ferramentas utilizadas no mercado para dar algumas dessas possíveis respostas.
Medidas de Risco e Volatilidade
O intuito desse post é levantar as medidas de risco disponível. Nesse sentido, não iremos aprofundar a discussão sobre a diferença entre risco e incerteza, tal como apresentada na teoria keynesiana. Acerca dessas medidas de risco e volatilidade, iremos utilizar duas métricas. A primeira é o drawdown, que informa a queda percentual máxima desde o último pico no preço das ações. A segunda é a Volatilidade, que é de maneira simples e direta o grau de oscilação percentual que temos no preço desses mesmos ativos.
Drawdown
Vamos aqui conceituar o Drawdown. Ela é a medida da queda percentual partindo de um pico histórico no preço de um ativo. Matematicamente ele pode ser expresso por:
\[D(T)=\max\left[\max_{t\in(0,T)}X(t)-X(T),0\right]\]
onde: \(D(T)\) é a medida de drawdown no tempo \(T\), \(X(t)\) é o retorno acumulado em um processo estocástico no período \(t\), sendo \(t\in(0,T)\) e \(X(T)\) o retorno acumulado em \(T\). Isso posto, vamos obter os dados do ibovespa no script abaixo e avaliar os drawdowns de 2007 até hoje. Para isso, faremos uso dos pacotes: BatchGetSymbols, xts e PerformanceAnalytics. O primeiro é utilizado para obter o histórico de preços (no caso pontos) do Ibovespa. Os dados são obtidos do yahoo finance e o histórico é apenas de 2007 para frente. Não é a base indicada para estudos longos, mas é uma disponível gratuitamente para download! O segundo é para transformar os dados de formato data.frame da em uma série temporal descontínua. O terceiro é um pacote de ferramentas, no qual inclui as funções para calcular o retorno diário e os drawdowns.
library(BatchGetSymbols)
library(xts)
library(PerformanceAnalytics)
Dados <- BatchGetSymbols(tickers = "^BVSP",
first.date = '2007-01-01',
last.date = Sys.Date(),
do.cache = FALSE)
IBOV <- xts(Dados$df.tickers$price.adjusted, order.by = Dados$df.tickers$ref.date)
IBOV <- na.omit(IBOV)Algumas notas sobre o script acima: A função BatchGetSymbols faz o download da série solicitada. Deixei a última data para utilizar a função Sys.Date() para tentar capturar o último dado disponível, sendo ele a data de hoje (flexível). Além disso, deixo o argumento do.cache como falso para evitar erros de sobreposição de valores entre o que é baixado e o que se encontra no cache previamente baixado.
Nas duas últimas linhas do script, crio uma série chamada IBOV em formato xts (série temporal irregular). Utilizo para as observações diárias o preço ajustado para dividendos, demais emolumentos, splits e agrupamentos. São ordenadas pelo vetor datas também disponível nos dados baixados. Na última linha, solicito a remoção de dias que não há observação na série.
Na sequência, plotamos o Ibovespa, calculamos o retorno diário de forma discreta \(\Delta P_t/P_{t-1}\), pedimos o cálculo da série de drawdowns, inputando os retornos diários e na sequência o plot. Por fim, pedimos para tabelar os 10 maiores drawdowns no período.
plot(IBOV)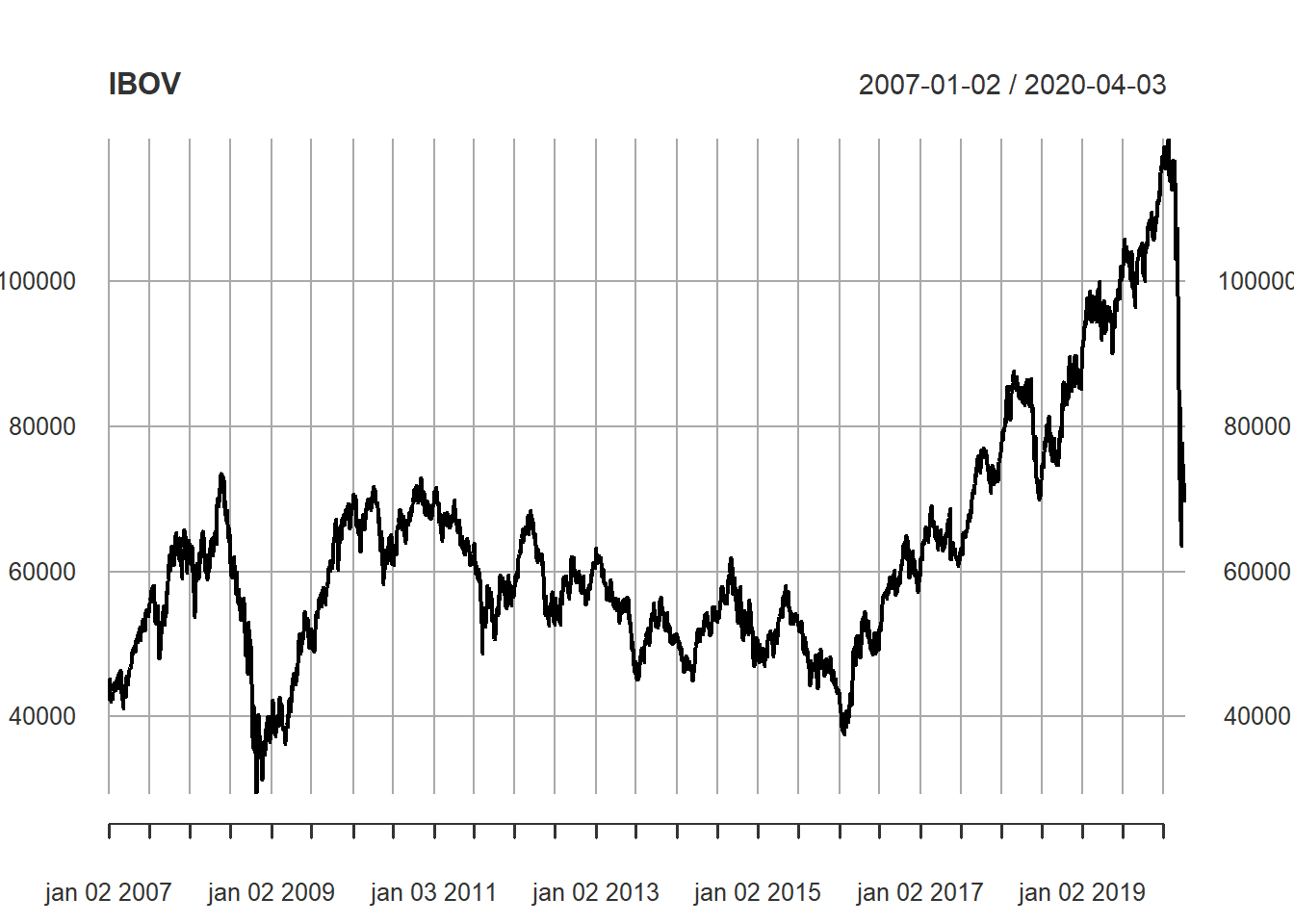
IBOV_ret <- Return.calculate(IBOV, method = "discrete")
IBOV_Dr <- PerformanceAnalytics::Drawdowns(IBOV_ret)
plot(IBOV_Dr, main = "Drawdown no Ibovespa")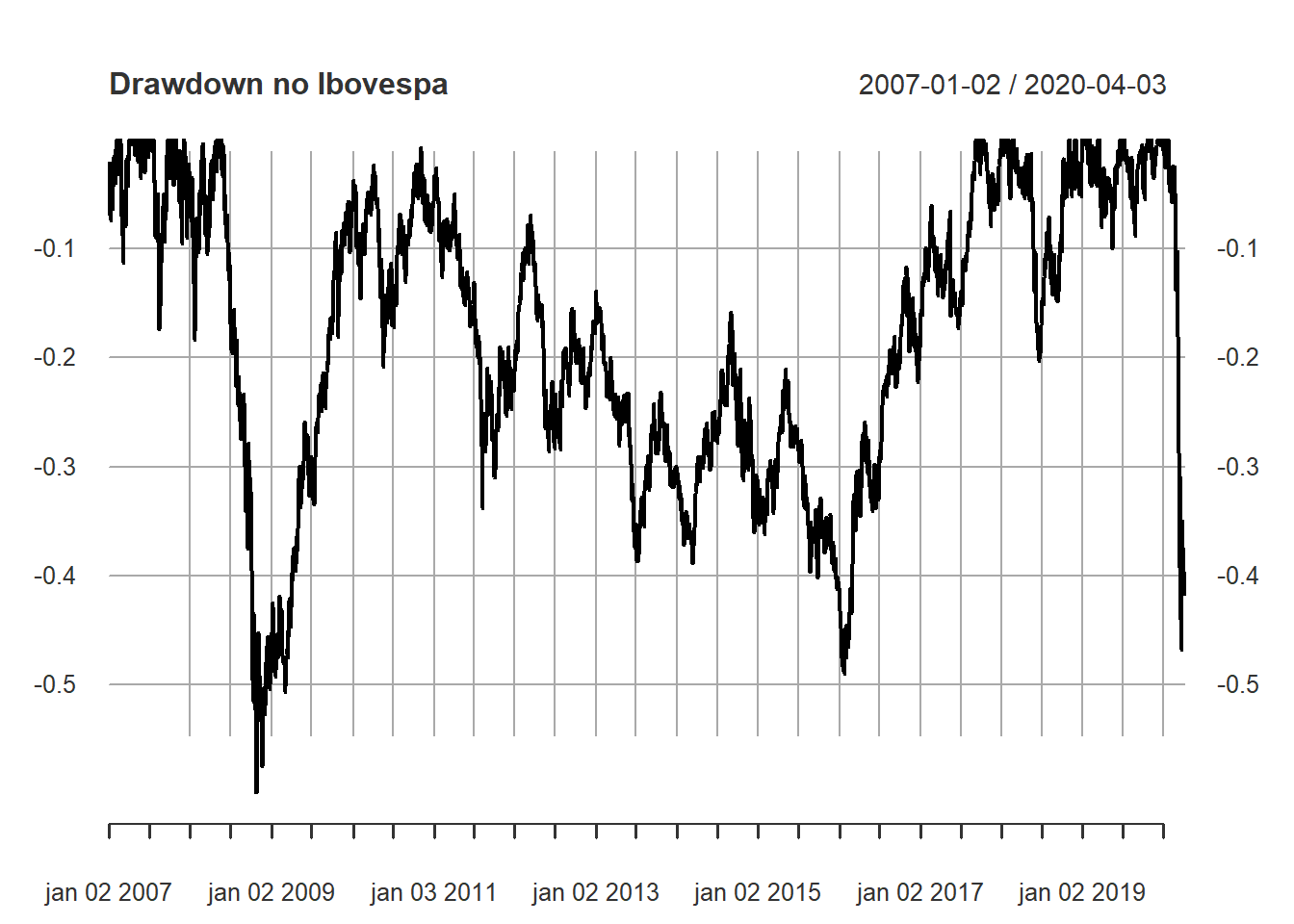
PerformanceAnalytics::table.Drawdowns(IBOV_ret, top = 10)## From Trough To Depth Length To Trough Recovery
## 1 2008-05-21 2008-10-27 2017-09-11 -0.5996 2306 112 2194
## 2 2020-01-24 2020-03-23 <NA> -0.4682 49 39 NA
## 3 2018-02-27 2018-06-18 2018-11-01 -0.2035 172 77 95
## 4 2007-12-07 2008-01-21 2008-04-30 -0.1836 95 28 67
## 5 2007-07-20 2007-08-16 2007-09-24 -0.1739 46 20 26
## 6 2007-02-23 2007-03-05 2007-04-04 -0.1135 29 7 22
## 7 2019-03-19 2019-05-17 2019-06-19 -0.1000 65 42 23
## 8 2007-11-01 2007-11-26 2007-12-06 -0.0957 23 15 8
## 9 2019-07-11 2019-08-26 2019-10-21 -0.0887 73 33 40
## 10 2017-10-16 2017-11-14 2018-01-02 -0.0800 53 21 32Sobre a tabela acima, algumas observações podem ser feitas. A maior queda histórica se deu em quem comprou na máxima, datada no dia 21/05/2008. Seu prejuízo só foi recuparado (em termos nominais) em 11/09/2017. A duração foi de 2306 dias, algo em torno de 10 anos. O tempo de mergulho durou 112 dias, algo em torno de 4 meses. A recuperação em si foi de 2194 dias de pregão. Outros casos são apontados na tabela, sendo o primeiro o maior -59,96%. Um detalhe importante tabelado é que o segundo maior drawdown foi aberto recentemente no dia 24/01/2020. Houve um mergulho de 39 dias, está durando 49 e não fechou a recuperação.
PerformanceAnalytics::AverageDrawdown(IBOV_ret)## [,1]
## Average Drawdown 0.04592626PerformanceAnalytics::AverageLength(IBOV_ret)## [,1]
## Average Length 50.20312Sobre as informações relativas ao drawdown médio e duração média deles, temos: 4,59% e 50,20 dias de pregão.
Volatilidade Histórica
Na literatura de finças, a volatilidade é medida através do desvio-padrão de uma série de retornos de um ativo. tomando como base a curva normal, quando maior for o desvio-padrão do retorno de uma série, maior o risco envolvido nela. Evidentemente, há críticas a essa forma de mensuração. Todavia, esse é um assunto mais extenso que não será explorado aqui, especificamente.
Antes de apresentar os modelos que serão utilizados, segue aqui uma ideia: Se o risco pode ser medido através do desvio-padrão do retorno de uma ação, o que aconteceria se essa medida variasse no tempo? Certamente, precisaríamos de um método que possua a flexibilidade de ser tempo variante.
Alias, para mostrar como o desvio-padrão é tempo variante, veja a série de retornos diários do Ibovespa:
plot(IBOV_ret)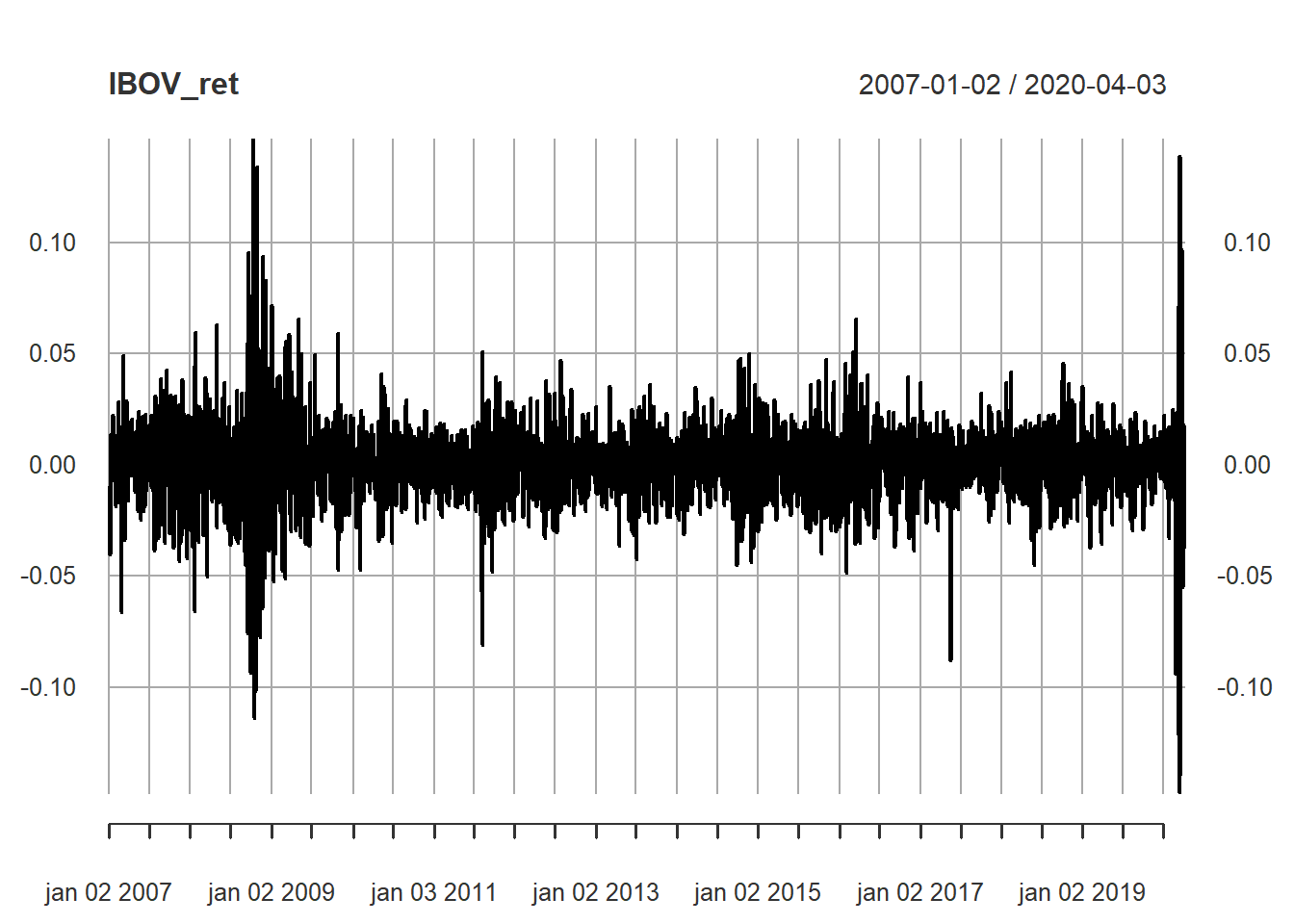
Pode-se perceber na figura acima que períodos entre 2008 e 2009 houve forte aumento da variação percentual diária nos preços, bem como em 2020. Chamamos isso na literatura de Clusters de Volatilidade ou (Agrupamento de Volatilidade).
Modelos ARCH/GARCH
O termo ARCH é uma abreviação traduzida de Modelo de Heterocedasticidade Condicional Auto Regressiva. Intuitivamente, o modelo captura o aumento da variância (heterocedasticidade) no tempo a partir termos autoregressivos. Ná prática é como se dias de calmaria chamassem novos dias de calmaria e dias de turbulência chamassem novos dias de turbulência. O modelo ARCH(1) pode ser representado matematicamente como1: \[y_t=\phi+e_t\] \[e_t|I_{t-1} \sim N(0,h_t)\] \[h_t=\alpha_0+\alpha_1.e^2_{t-1}, \alpha_0>0, 0\leq\alpha_1<1 \]
O primeiro passo para verificar se os nossos dados sofrem influência do efeito de heterocedasticidade condicional é realizar o teste ARCH. Tal como proposto por Colonesco (2016), iremos fazê-lo de duas formas: (1) Abrindo o teste no passo-a-passo e; (2) Teste direto apenas obtendo o report.
Dessa forma, faremos uso dos pacotes: dynlm, broom, FinTS e tseries.
library(dynlm)
library(broom)
library(FinTS)
library(tseries)
Ibov_Med <- dynlm(as.zoo(IBOV_ret)~1)
summary(Ibov_Med)##
## Time series regression with "zoo" data:
## Start = 2007-01-03, End = 2020-04-03
##
## Call:
## dynlm(formula = as.zoo(IBOV_ret) ~ 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.148092 -0.008748 0.000384 0.009256 0.146265
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0002952 0.0003168 0.932 0.351
##
## Residual standard error: 0.01813 on 3274 degrees of freedom
## (1 observation deleted due to missingness)ehatsq <- ts(resid(Ibov_Med)^2)
IBOV.ARCH <- dynlm(ehatsq~L(ehatsq))
summary(IBOV.ARCH)##
## Time series regression with "ts" data:
## Start = 2, End = 3275
##
## Call:
## dynlm(formula = ehatsq ~ L(ehatsq))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.0079604 -0.0002326 -0.0001733 0.0000076 0.0205867
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.047e-04 1.879e-05 10.89 <2e-16 ***
## L(ehatsq) 3.774e-01 1.619e-02 23.31 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.001031 on 3272 degrees of freedom
## Multiple R-squared: 0.1424, Adjusted R-squared: 0.1421
## F-statistic: 543.2 on 1 and 3272 DF, p-value: < 2.2e-16T <- nobs(Ibov_Med)
q <- length(coef(IBOV.ARCH))-1
Rsq <- glance(IBOV.ARCH)[[1]]
LM <- (T-q)*Rsq
alpha <- 0.05
Chicr <- qchisq(1-alpha, q)
# Report das Variáveis
LM## [1] 466.1533Chicr## [1] 3.841459O script acima abre o chamado teste ARCH de heterocedasticidade condicional. Começamos o script carregando os pacotes, estimamos através da função dynlm a série de retornos diários do IBOV contra uma constante. Reportamos o resultado. Na sequência, montamos uma série da variância da série, elevando ao quadrado o resíduo obtido da equação anterior.
Tendo sido estimada a variância, estimamos a variância em \(t\) frente suas primeira defasagem. Reportamos e separamos os valores \(T\) (tamanho da série); \(q\) a quantidade de coeficientes estimados; \(R^2\) da Regressão (variável Rsq). O valor \(LM\) obtido é igual a \((T-q).R^2\); o alpha será de 5%; Obtemos o valor de \(\chi^2\) para os parâmetros \((1-\alpha,q)\).
O resultado da Estatística \(LM=466,15\), que deve ser comparada com o valor crítico \(\chi^2_{(0.95,1)}=(3,84)\). Isso indica que a hipótese nula deve ser rejeitada, concluindo que a série sofre de efeito \(ARCH\).
Mais formalmente, o teste se baseia em testar as seguintes hipóteses: \[\hat{e}_t^2=\gamma_0+\gamma_1.\hat{e}_{t-1}^2+...+\gamma_q.\hat{e}_{t-q}+v_t\] No qual as Hipóteses Nula e Alternativa do Teste ARCH: \[H_0:\gamma_1=...=\gamma_q=0\] \[H_A:\gamma_i \neq0 \forall i\in \left[ 1,2,...,q\right] \] Portanto, aceitar a hipótese nula é admitir que a série não sofra de heterocedasticidade condicional autoregressiva, enquanto que rejeitar a hipótese nula é aceitar que sofra de heterocedasticidade condicional autoregressiva.
ArchTest(IBOV_ret, lags=1, demean=TRUE)##
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: IBOV_ret
## Chi-squared = 466.15, df = 1, p-value < 2.2e-16IBOV.GARCH <- invisible(garch(na.omit(IBOV_ret),c(1,1)))##
## ***** ESTIMATION WITH ANALYTICAL GRADIENT *****
##
##
## I INITIAL X(I) D(I)
##
## 1 2.958252e-04 1.000e+00
## 2 5.000000e-02 1.000e+00
## 3 5.000000e-02 1.000e+00
##
## IT NF F RELDF PRELDF RELDX STPPAR D*STEP NPRELDF
## 0 1 -1.164e+04
## 1 7 -1.166e+04 1.25e-03 1.88e-03 3.3e-04 2.1e+10 3.3e-05 1.96e+07
## 2 8 -1.166e+04 6.63e-05 9.68e-05 3.0e-04 2.0e+00 3.3e-05 1.26e+02
## 3 9 -1.166e+04 1.33e-05 1.39e-05 3.2e-04 2.0e+00 3.3e-05 1.24e+02
## 4 16 -1.174e+04 6.79e-03 1.15e-02 4.4e-01 2.0e+00 7.9e-02 1.23e+02
## 5 19 -1.183e+04 7.81e-03 9.03e-03 6.4e-01 2.0e+00 2.2e-01 9.46e+00
## 6 25 -1.183e+04 1.38e-04 6.94e-04 2.7e-05 1.4e+02 1.5e-05 2.69e-01
## 7 26 -1.183e+04 6.89e-05 6.06e-05 2.5e-05 2.0e+00 1.5e-05 2.88e-02
## 8 27 -1.183e+04 1.39e-06 1.42e-06 2.6e-05 2.0e+00 1.5e-05 2.96e-02
## 9 36 -1.193e+04 7.86e-03 7.40e-03 3.0e-01 5.7e-01 2.5e-01 2.93e-02
## 10 38 -1.195e+04 1.84e-03 1.73e-03 4.4e-02 2.0e+00 4.9e-02 1.72e-01
## 11 40 -1.198e+04 3.06e-03 3.29e-03 7.8e-02 1.9e+00 9.9e-02 4.63e-01
## 12 42 -1.199e+04 3.92e-04 5.39e-04 1.4e-02 1.8e+00 2.0e-02 5.88e-03
## 13 44 -1.200e+04 8.72e-04 1.09e-03 2.9e-02 1.6e+00 4.1e-02 6.12e-03
## 14 45 -1.200e+04 4.42e-04 5.35e-04 2.7e-02 7.2e-01 4.1e-02 7.74e-04
## 15 46 -1.201e+04 6.24e-04 3.47e-04 1.8e-02 0.0e+00 3.6e-02 3.47e-04
## 16 47 -1.202e+04 5.74e-04 2.23e-03 6.2e-02 7.3e-01 1.5e-01 3.38e-03
## 17 58 -1.202e+04 1.13e-04 3.69e-03 2.3e-06 2.4e+00 4.2e-06 5.69e-03
## 18 59 -1.203e+04 9.53e-04 6.77e-04 8.8e-07 2.0e+00 2.1e-06 2.74e-03
## 19 60 -1.203e+04 8.71e-05 1.37e-04 9.7e-07 2.0e+00 2.1e-06 9.67e-04
## 20 61 -1.203e+04 1.56e-05 1.76e-05 1.1e-06 2.0e+00 2.1e-06 8.29e-04
## 21 62 -1.203e+04 2.28e-07 2.21e-07 1.1e-06 2.0e+00 2.1e-06 8.00e-04
## 22 69 -1.203e+04 1.42e-04 2.68e-04 4.7e-03 1.1e+00 8.6e-03 7.98e-04
## 23 71 -1.204e+04 8.72e-05 1.38e-04 7.6e-03 8.7e-01 1.7e-02 2.65e-04
## 24 72 -1.204e+04 3.94e-06 3.19e-06 1.4e-03 0.0e+00 2.7e-03 3.19e-06
## 25 73 -1.204e+04 2.95e-07 2.78e-07 4.5e-04 0.0e+00 8.7e-04 2.78e-07
## 26 74 -1.204e+04 3.05e-09 2.93e-09 3.1e-05 0.0e+00 6.1e-05 2.93e-09
## 27 75 -1.204e+04 1.38e-10 1.39e-10 3.3e-07 0.0e+00 7.3e-07 1.39e-10
## 28 76 -1.204e+04 3.72e-12 3.21e-12 3.9e-07 1.4e+00 7.3e-07 4.46e-12
##
## ***** RELATIVE FUNCTION CONVERGENCE *****
##
## FUNCTION -1.203567e+04 RELDX 3.876e-07
## FUNC. EVALS 76 GRAD. EVALS 29
## PRELDF 3.207e-12 NPRELDF 4.457e-12
##
## I FINAL X(I) D(I) G(I)
##
## 1 6.676347e-06 1.000e+00 -1.118e+02
## 2 8.252343e-02 1.000e+00 -4.013e-02
## 3 8.943420e-01 1.000e+00 -4.761e-02summary(IBOV.GARCH)##
## Call:
## garch(x = na.omit(IBOV_ret), order = c(1, 1))
##
## Model:
## GARCH(1,1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.06093 -0.56924 0.04532 0.62291 4.18402
##
## Coefficient(s):
## Estimate Std. Error t value Pr(>|t|)
## a0 6.676e-06 1.133e-06 5.89 3.85e-09 ***
## a1 8.252e-02 7.226e-03 11.42 < 2e-16 ***
## b1 8.943e-01 9.609e-03 93.07 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Diagnostic Tests:
## Jarque Bera Test
##
## data: Residuals
## X-squared = 662.09, df = 2, p-value < 2.2e-16
##
##
## Box-Ljung test
##
## data: Squared.Residuals
## X-squared = 1.0251, df = 1, p-value = 0.3113hhat <- ts(2*IBOV.GARCH$fitted.values[-1,1]^2)
plot(hhat, main = "Série Estimada por GARCH(1,1) da Variância Condicional",
col = "red", ylab = "Variância do Retorno Diário", xlab = "Tempo")
grid(nx = NULL, ny = NULL, lty = "dotted", col = "grey")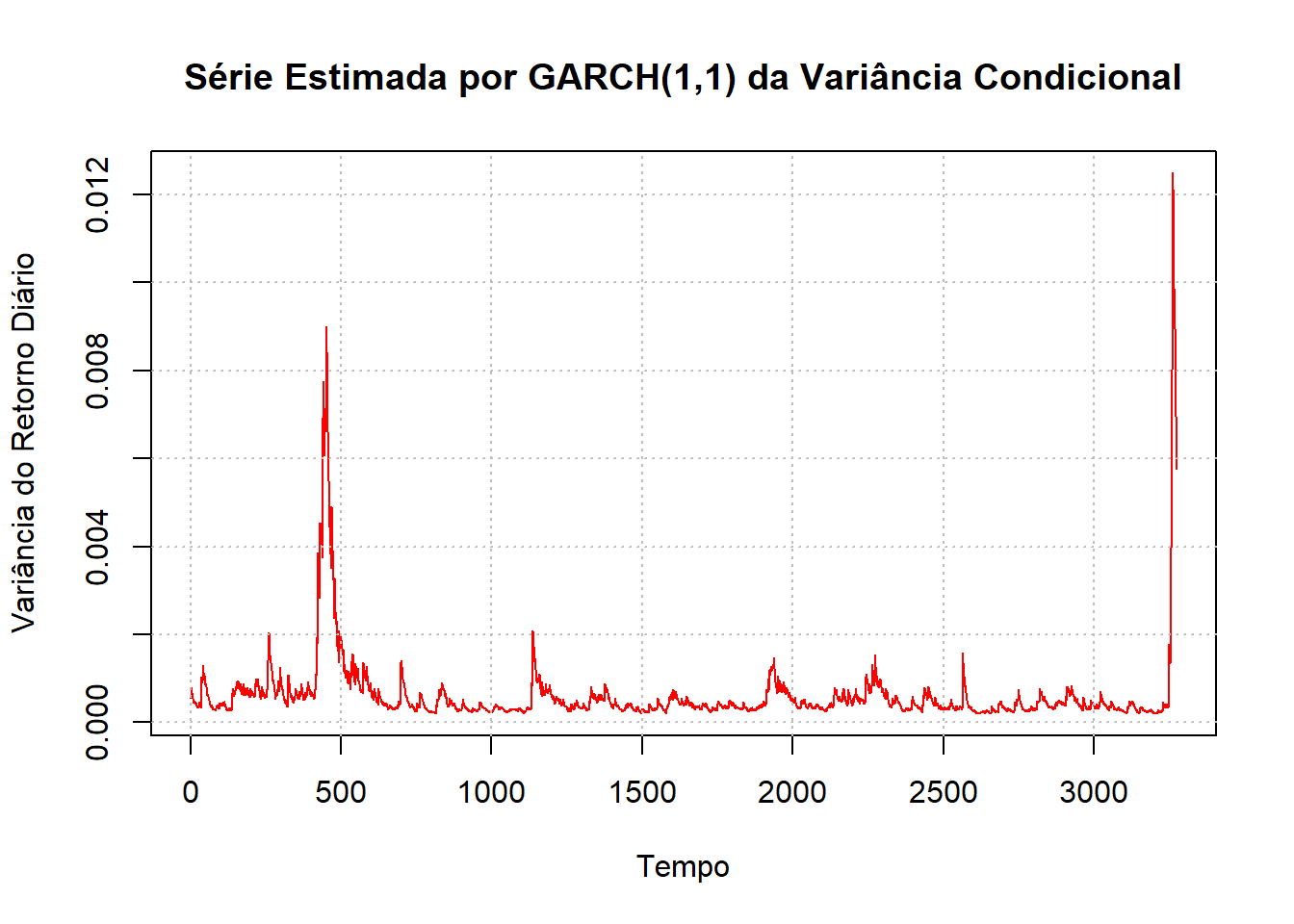
plot(hhat^(0.5), main = "Volatilidade Estimada por GARCH(1,1)",
col = "blue", ylab = "Desvio-Padrão do Retorno Diário", xlab = "Tempo")
grid(nx = NULL, ny = NULL, lty = "dotted", col = "grey")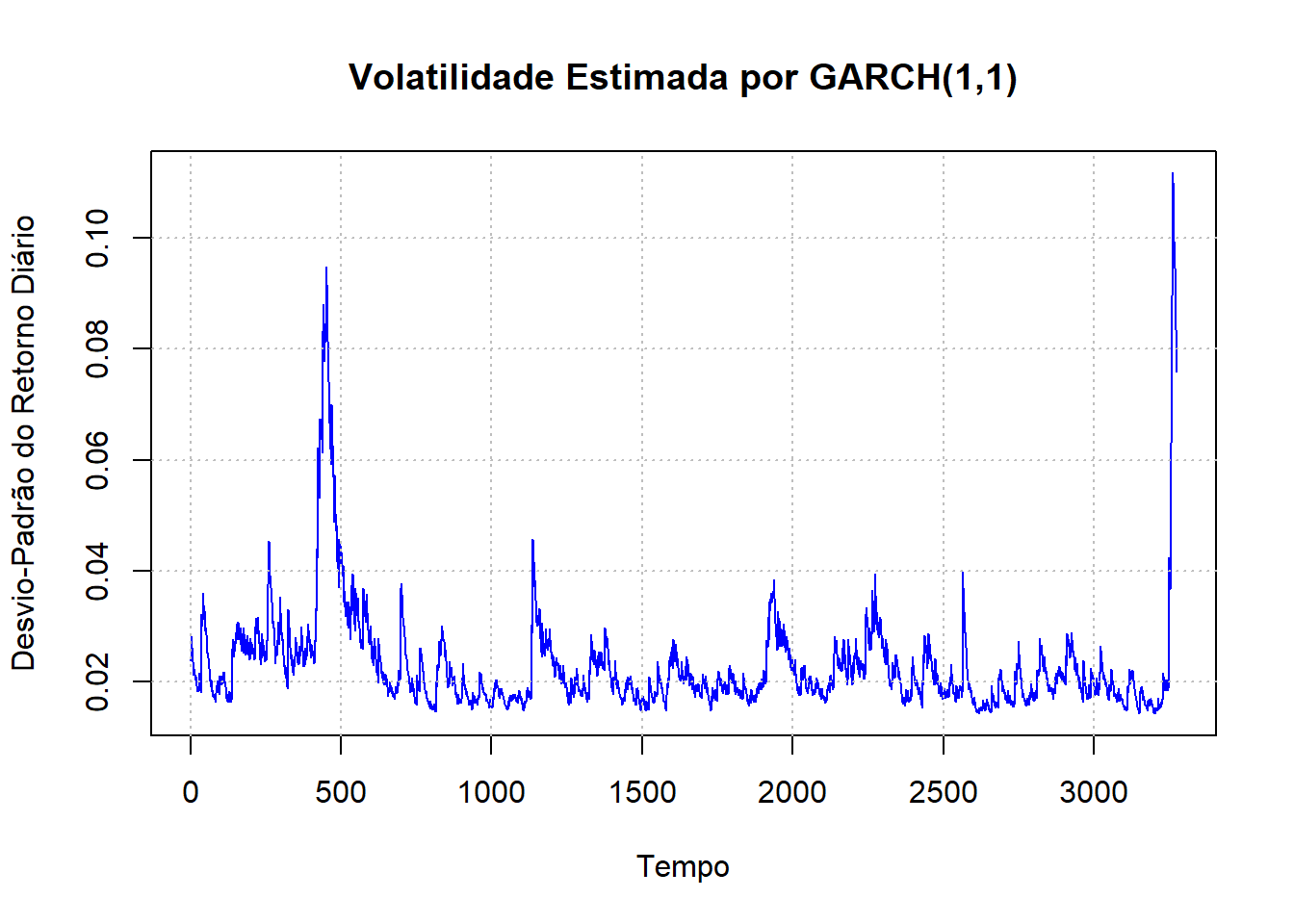
O último gráfico com título de Volatilidade Estimada por GARCH(1,1) é o que nos interessa ao fim. Ele aponta como a volatilidade do IBOV hoje pode ser comparada a que tivemos no passado. Nesse momento, podemos ver que já passamos o valor observado no período da crise Subprime. Portanto, não seria exagero falar que os últimos dias já podem ser considerados como a maior crise financeira (no sentido de impacto aos mercados financeiros) das duas últimas décadas.
Referências
COLONESCU, C. Principles of Econometrics with R. Disponível em https://bookdown.org/ccolonescu/RPoE4/time-varying-volatility-and-arch-models.html. 2016.
É mais intuitivo entender a especificação de uma defasagem. Evidentemente, podemos expandir a notação para \(q\) defasagens, bem como \(y_t\) pode ter um processo estilo \(ARMA(p,q)\).↩