Introdução ao Modelo CAPM (Capital Asset Pricing Model)
Introdução
Um dos modelos mais famosos na área de Finanças é o conhecido CAPM (Capital Asset Pricing Model). Ele data sua origem no trabalho de Treynor, Sharpe, Lintner e Mossin.
Formulação Matemática
Para derivar o modelo CAPM de uma forma mais rigorosa, nós utilizaremos um resultado encontrado na resolução de um portfólio ótimo quando é permitida venda a descoberto.1
A resolução do problema envolve encontrar a composição do portfólio que maximiza a inclinação da reta que passa entre a taxa livre de risco (no eixo vertical) e o próprio portfólio. Mais formalmente, isso envolveria maximizar a função:
\[\theta=(\overline{R}_P-R_F)/\sigma_P \] Sujeita a seguinte restrição: \[\sum_{i=1}^N X_i=1\] onde \(X_i\) é o percentual do ativo \(i\in[1,2,...,N]\).; \(\overline{R}_P\) é o retorno esperado do portfólio; \(R_F\) é o retorno livre de risco e \(\sigma_P\) é o desvio-padrão do portfólio (medida de risco).
Ou seja, estamos maximizar a unidade de medida que captura a fração entre prêmio de risco sobre o risco envolvido.
Repare que a mesma função acima pode ser aberta nos \(N\) ativos que a compoem. Ficando:
\[\theta=\frac{\sum_{i=1}^N X_i.(\overline{R}_i-R_F)}{(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j})^{1/2}} \] A solução do problema de maximação exige como condição que: \[\begin{array}{c} \partial\theta/\partial X_1=0 \\ \partial\theta/\partial X_2=0 \\ ... \\ \partial\theta/\partial X_N=0 \end{array}\] Onde as derivadas de \(\theta\) com relação a \(X_i\) são2: \[\partial\theta/\partial X_i=-\lambda.(X_1.\sigma_{1i}+X_2.\sigma_{2i}+...+X_N.\sigma_{Ni}+X_i.\sigma_{i}^2)+\overline{R}_i-R_F=0\]
Repare que a condição da equação anterior vale para cada ação e, portanto, há uma equação para cada ação no mercado. Se houver expectativas homogêneas, então todos os investidores devem selecionar o mesmo portfólio ótimo. Se todos os investidores selecionam o mesmo portfólio, então, em equilíbrio, esse portfólio deve ser um portfólio no qual todas as ações estão na mesma percentagem que são representadas no mercado. Em outras palavras, em equilíbrio, a proporção investida na ação 1 deve ser a mesma fração que representa o valor de mercado que a ação 1 representa no total.
Para partir da equação acima em direção ao CAPM, devemos reconhecer que o lado esquerdo da equação é o mesmo que \(\lambda.cov(R_k.R_M)\). Para enxergar isso, repare que3: \[R_M=\sum_ {i=1}^N R_i.X_i'\] Assim, temos que: \[cov(R_k,R_M)=E\left[(R_k-\overline{R}_k).\left(\sum_{i=1}^NR_i.X_i' -\sum_{i=1}^N\overline{R}_i.X_i' \right) \right] \] Rearranjando o segundo termo, temos: \[cov(R_k,R_M)=E\left[(R_k-\overline{R}_k).\left(\sum_{i=1}^NX_i'.(R_i-\overline{R}_i) \right) \right] \] Abrindo os termos da multiplicação, temos: \[cov(R_k,R_M)=E[X_1'.E(R_k-\overline{R}_k).(R_1-\overline{R}_1)+...\] \[...+X_k'.E(R_k-\overline{R}_k)^2+...+X_N'.E(R_k-\overline{R}_k).(R_N-\overline{R}_N)]\]
Previamente, argumentamos que \(X_i'\) são as proporções de mercado. Comparando a equação anterior com o primeiro termo da derivada \(\partial\theta/\partial X_i\) temos uma igualdade. Assim, a equação que formula a condição de equilíbrio pode ser reescrita como: \[\lambda.cov(R_k,R_M)=\overline{R}_k-R_F\] Devido a condição ser a mesma para todas as ações (todos possíveis valores de \(k\)), temos como implicação que ela também a seja para todos os portfólios de ações. Um possível portfólio é o portfólio de mercado. Escrevendo a equação acima para o portfólio de mercado e substituindo \(cov(R_M,R_M)=\sigma_M^2\), temos: \[\lambda=\frac{\overline{R}_M-R_F}{\sigma_M^2}\] Substituindo esse valor para \(\lambda\) na equação de equilibrio para \(R_k\) e reorganizando-a, temos: \[\overline{R}_k=R_F+\frac{\overline{R}_M-R_F}{\sigma_M^2}.cov(R_k,R_m)\] Ou ainda \[\overline{R}_k=R_F+\beta_k.(\overline{R}_M-R_F)\] Isso completa uma forma de derivar a SML (Security Market Line) e consequentemente a equação geral do modelo CAPM. O que ela informa é que o retorno médio de um ativo \(k\) é explicado pelo retorno livre de risco (nossa Selic diária, por exemplo) mais um coeficiente que capta a sensibilidade ao prêmio de risco (Retorno de mercado menos o retorno livre de risco).
Análise do Modelo Utilizando o R
Apresentada a formulação matemática do modelo CAPM, vamos agora verificar a utilização dele para analisar algumas ações da B3. Para isso, faremos uso dos seguintes pacotes: xts, PerformanceAnalytics, xtsanalytics, BETS e stargazer.
O segundo pacote é para lidar com séries temporais descontínuas (intervalos irregulares como ocorre na bolsa), o segundo é um pacote de ferramentas para análise de ações e do portfólio, o terceiro é um pacote recente, muito útil, que facilita a organização dos dados baixados do yahoo finance, o quarto é para baixar a série temporal diária da Selic e a última é para juntar dados de regressões em uma tabela só.
O código começa limpando os dados anteriores através do comando rm(list=ls()).
rm(list=ls())
library(xts)
library(PerformanceAnalytics)
library(xtsanalytics)
library(BETS)
library(stargazer)
library(kableExtra)
#remotes::install_github("jeanmarcgp/xtsanalytics")
Busca <- BETSsearch("interest rate")
kable(head(Busca)) %>%
kable_styling(bootstrap_options = "striped", full_width = F)| code | description | unit | periodicity | start | last_value | source |
|---|---|---|---|---|---|---|
| 1002 | Credit operations with nonearmarked funds (floating rate) - Acquisition of vehicles-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
| 1015 | Credit operations with nonearmarked funds (based on price index rate) - Acquisition of vehicles-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
| 1027 | Credit operations with nonearmarked funds (preset rate) - Acquisition of other goods-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
| 1038 | Credit operations with nonearmarked funds (postset rate) - Acquisition of other goods-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
| 1050 | Credit operations with nonearmarked funds (floating rate) - Acquisition of other goods-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
| 1063 | Credit operations with nonearmarked funds (based on price index rate) - Acquisition of other goods-individuals - Interest rate | % p.d. | D | 31/05/2000 | 31/12/2012 | Sisbacen PESP300 |
Na sequência fazemos uma busca geral nas bases do BETS, através da função `BETSsearch() para séries de taxa de juros. Ao olhar no resultado da busca, verificamos que o código 11 é referente a taxa Selic em taxa e observações diárias. Posteriormente, fazemos o download através do comando BETSget() e transformamos em série temporal através da função xts().
Uma vez obtida nossa taxa básica, o próximo passo é obter a série de preços das ações. Escolhemos ad hoc as ações ITUB4, WEGE3, B3SA, ABEV3, PETR4. Como retorno do mercado, utilizamos como proxy o índice Ibovespa. Fazemos o dowload dessas séries com os preços ajustados através da função mget_symbols(). Obtidos os preços, calculamos os retornos diários através da função Return.calculate() e na sequência juntamos com a série da taxa selic diária.
Para alinhar os ativos para que todos tivessem as mesmas observações, utilizamos o comando na.omit(). Criamos a série de prêmio de risco como sendo a diferença entre a rentabilidade do mercado (Ibov) menos o retorno da taxa selic.
# Selic Diária em valor percentual a.d.
Selic_Dia <- BETSget(code = "11")
Ret_Livre_Risco <- xts(Selic_Dia$value*0.01, order.by = Selic_Dia$date)
Ativos <- cbind("ITUB4.SA",
"WEGE3.SA",
"B3SA3.SA",
"ABEV3.SA",
"PETR4.SA",
"^BVSP")
Precos <- mget_symbols(Ativos, OHLC = "Ad")## Getting data from yahoo...
## Downloading symbols: ITUB4.SA WEGE3.SA B3SA3.SA ABEV3.SA PETR4.SA ^BVSP
##
## Successfully downloaded symbol: ITUB4.SA
## Successfully downloaded symbol: WEGE3.SA
## Successfully downloaded symbol: B3SA3.SA
## Successfully downloaded symbol: ABEV3.SA
## Successfully downloaded symbol: PETR4.SA
## Successfully downloaded symbol: ^BVSP
##
##
## DOWNLOAD SUMMARY:
## =================
## Symbols successfully downloaded: ITUB4.SA WEGE3.SA B3SA3.SA ABEV3.SA PETR4.SA BVSP
## Symbols NOT downloaded:
##
## Applying na.locf to the matrix...Retornos <- Return.calculate(Precos, method = "discrete")
Serie <- cbind(Ret_Livre_Risco,Retornos)
Retornos <- na.omit(Serie)
Retornos$Premio_Risco <- Retornos$BVSP - Retornos$Ret_Livre_RiscoNa sequência, obtemos o resultado de regressões por MQO do retorno diário da ação contra o prêmio de risco e o retorno livre de risco. A regressão é estimada sem intercepto.
ITUB4.fit <- lm(`ITUB4.SA` ~ Premio_Risco + Ret_Livre_Risco -1, data = Retornos)
WEGE3.fit <- lm(`WEGE3.SA` ~ Premio_Risco + Ret_Livre_Risco -1, data = Retornos)
B3SA3.fit <- lm(`B3SA3.SA` ~ Premio_Risco + Ret_Livre_Risco -1, data = Retornos)
ABEV3.fit <- lm(`ABEV3.SA` ~ Premio_Risco + Ret_Livre_Risco -1, data = Retornos)
PETR4.fit <- lm(`PETR4.SA` ~ Premio_Risco + Ret_Livre_Risco -1, data = Retornos)Isso posto, agregamos os resultados das regressões na forma de tabela através da função stargazer(). Ela formata a tabela e a gera no formato HTML.
stargazer(ITUB4.fit,WEGE3.fit,B3SA3.fit,ABEV3.fit,PETR4.fit,
type = "html", digits = 3)| Dependent variable: | |||||
| ITUB4.SA | WEGE3.SA | B3SA3.SA | ABEV3.SA | PETR4.SA | |
| (1) | (2) | (3) | (4) | (5) | |
| Premio_Risco | 0.991*** | 0.575*** | 1.069*** | 0.525*** | 1.455*** |
| (0.015) | (0.022) | (0.020) | (0.018) | (0.026) | |
| Ret_Livre_Risco | 1.828*** | 2.771*** | 2.728*** | 1.634** | 1.607 |
| (0.664) | (0.958) | (0.862) | (0.763) | (1.127) | |
| Observations | 2,223 | 2,223 | 2,223 | 2,223 | 2,223 |
| R2 | 0.651 | 0.234 | 0.564 | 0.285 | 0.583 |
| Adjusted R2 | 0.651 | 0.234 | 0.564 | 0.285 | 0.583 |
| Residual Std. Error (df = 2221) | 0.012 | 0.017 | 0.015 | 0.014 | 0.020 |
| F Statistic (df = 2; 2221) | 2,075.932*** | 339.616*** | 1,437.908*** | 442.990*** | 1,554.108*** |
| Note: | p<0.1; p<0.05; p<0.01 | ||||
Regressões obtidas e apresentadas, vamos agora investigar visualmente a “cara” tem essas regressões. Para isso usamos, o pacote ggplot2 para plotar essas figuras.
library(ggplot2)
theme_set(theme_bw())
ggplot(data = Retornos, aes(y = `ITUB4.SA`, x = Premio_Risco)) +
geom_point(col='blue') +
xlab('Prêmio de Risco') +
ylab('Expectativa de Retorno') +
ggtitle('Retorno ITUB4') +
geom_smooth(method = "lm", se = T, col = "black")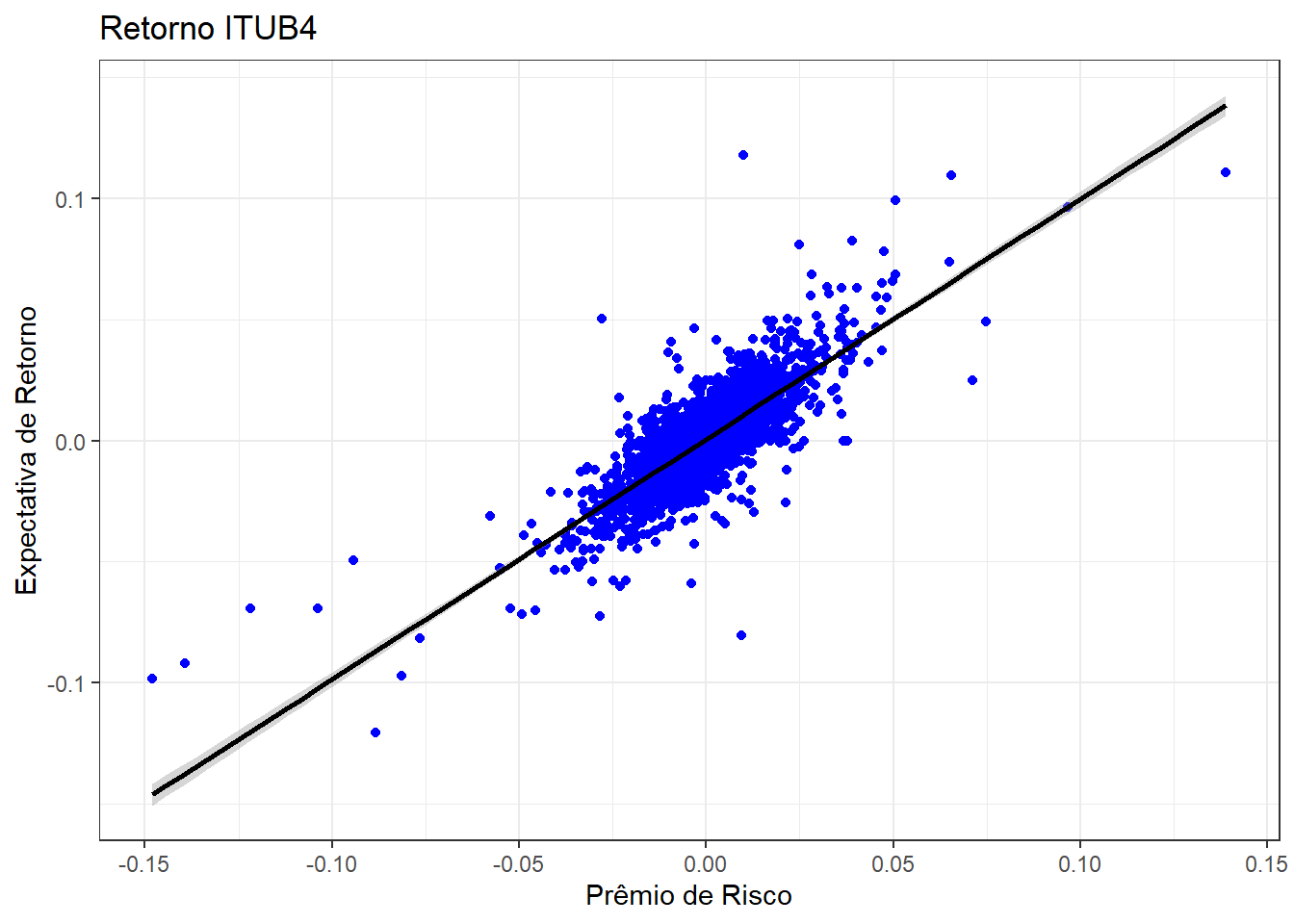
ggplot(data = Retornos, aes(y = `WEGE3.SA`, x = Premio_Risco)) +
geom_point(col=' dark green') +
xlab('Prêmio de Risco') +
ylab('Expectativa de Retorno') +
ggtitle('Retorno WEGE3') +
geom_smooth(method = "lm", se = T, col = "black") 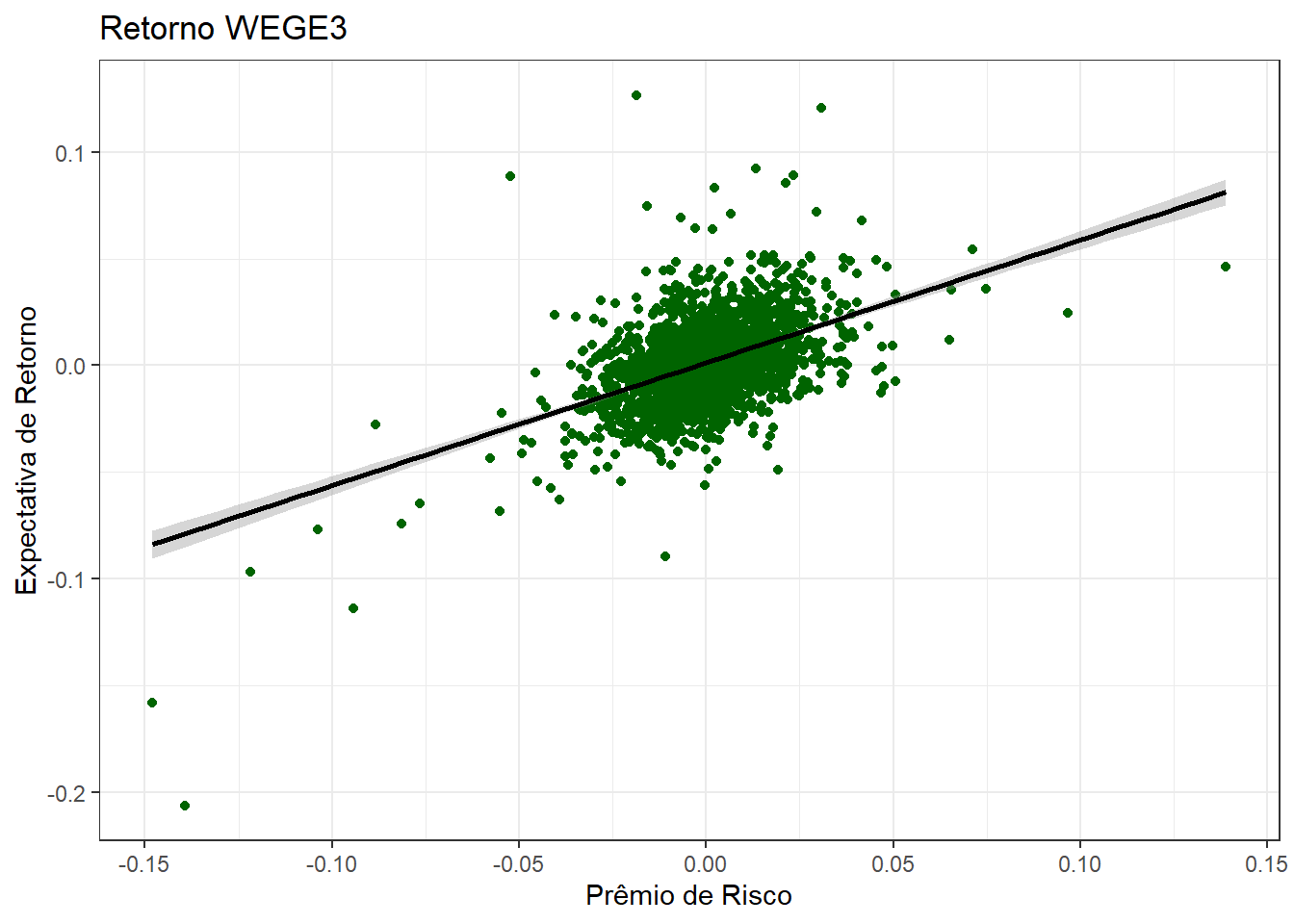
ggplot(data = Retornos, aes(y = `B3SA3.SA`, x = Premio_Risco)) +
geom_point(col='cyan') +
xlab('Prêmio de Risco') +
ylab('Expectativa de Retorno') +
ggtitle('Retorno B3SA3') +
geom_smooth(method = "lm", se = T, col = "black")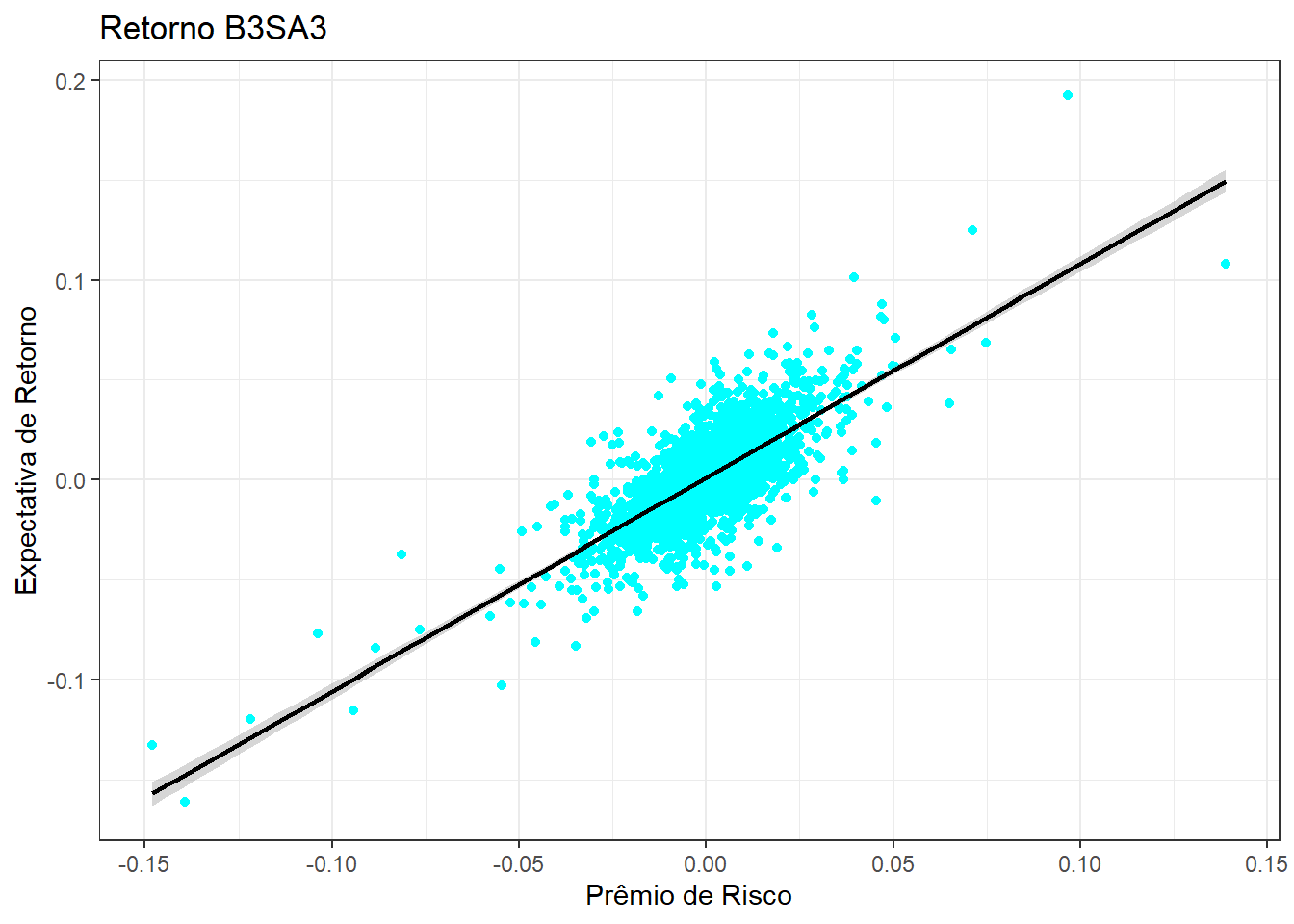
ggplot(data = Retornos, aes(y = `ABEV3.SA`, x = Premio_Risco)) +
geom_point(col='brown') +
xlab('Prêmio de Risco') +
ylab('Expectativa de Retorno') +
ggtitle('Retorno ABEV3') +
geom_smooth(method = "lm", se = T, col = "black")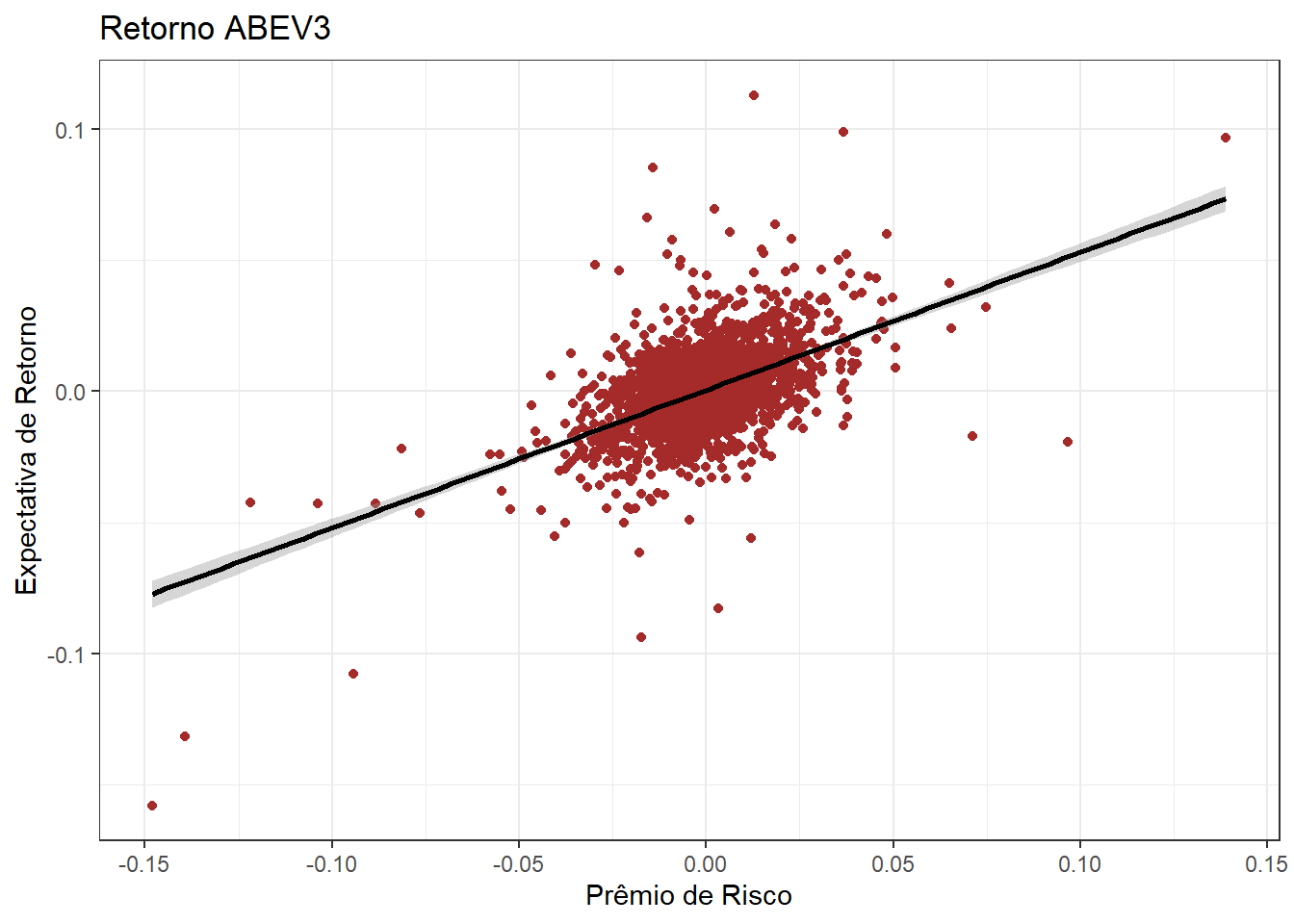
ggplot(data = Retornos, aes(y = `PETR4.SA`, x = Premio_Risco)) +
geom_point(col='orange') +
xlab('Prêmio de Risco') +
ylab('Expectativa de Retorno') +
ggtitle('Retorno PETR4') +
geom_smooth(method = "lm", se = T, col = "black")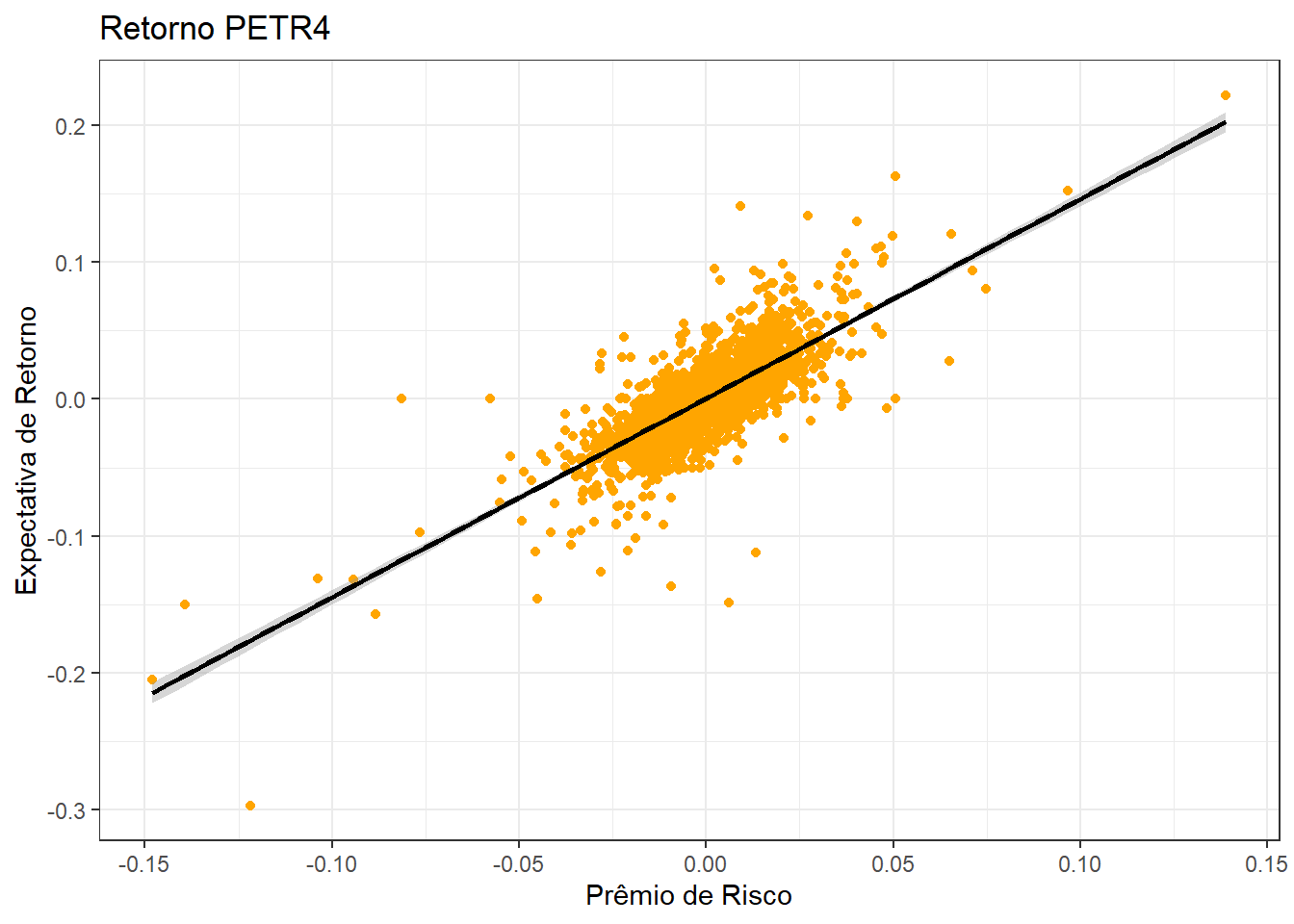
Referências
BANZ, R. W. The relationship between return and market value of common stocks. Journal of Financial Economics, v. 9, n. 1, p. 3-18, 1981.
BLACK, F.; JENSEN, M. C.; SCHOLES, M. The capital asset pricing model: some empirical tests. In: JENSEN, M. C. (Ed.). Studies in the Theory of Capital Markets. New York: Praeger, 1972. p. 79-121.
ROSS, S. A. The arbitrage theory of capital asset pricing. Journal of Economic Theory, v. 13, n. 3, p. 341-360. 1976.
SHARPE, W. F. Capital asset prices: a theory of market equilibrium under conditions of risk. Journal of Finance, v. 19, n. 3, p. 425- 442, 1964.
O investidor pode tomar dinheiro emprestado e emprestar quantias ilimitadas de dinheiro à taxa livre de risco para poder aplicar (ou aplicarem) no mercado de renda variável.↩
Obtenção detalhada da derivada: Reorganizando a função, temos que: \[\theta=\sum_{i=1}^N X_i.(\overline{R}_i-R_F).\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j}\right) ^{-1/2}\] Utilizando a derivada do produto na equação acima, obtemos: \[\frac{\partial[F_1(X).F_2(X)]}{\partial X}=F_1(X).\frac{\partial F_2(X)}{\partial X} + F_2(X).\frac{\partial F_1(X)}{\partial X}\] Sendo: \[F_1(X)=\sum_{i=1}^N X_i.(\overline{R}_i-R_F)\] e \[F_2(X)=\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j}\right) ^{-1/2}\] As respectivas derivadas são: \[\frac{\partial F_1(X)}{\partial X_k}= (\overline{R}_k-R_F)\] e \[\frac{\partial F_2(X)}{\partial X_k}=\left(-\frac{1}{2}\right).\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j} \right)^{-3/2}.\] \[.2.\left(X_k.\sigma_k^2+\sum_{j=1,j\neq k}^NX_j.\sigma_{j,k} \right)\] Observe que as derividas surgem com o termo \(k\). A ideia é que o portfólio esteja aumentando em mais uma ação e o quanto essa ação está proporcionando de risco e retorno a mais para o portfólio como um todo. Simplificando a última derivada: \[\frac{\partial F_2(X)}{\partial X_k}=-\frac{\left(X_k.\sigma_k^2+\sum_{j=1,j\neq k}^NX_j.\sigma_{j,k} \right)}{\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j} \right)^{3/2}}\] Juntando os termos, igualando a zero, temos: \[\frac{\partial\theta}{\partial X_k}=\frac{-\sum_{i=1}^N X_i.(\overline{R}_i-R_F).\left(X_k.\sigma_k^2+\sum_{j=1,j\neq k}^NX_j.\sigma_{j,k} \right)}{\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j} \right)^{3/2}} + \] \[+\frac{(\overline{R}_k-R_F)}{\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j}\right) ^{1/2}}\] Multiplicando por \(\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j}\right) ^{1/2}\) ambos os lados e simiplificando resulta em: \[\frac{\partial\theta}{\partial X_k}=-\frac{\sum_{i=1}^N X_i.(\overline{R}_i-R_F).\left(X_k.\sigma_k^2+\sum_{j=1,j\neq k}^NX_j.\sigma_{j,k} \right)}{\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j} \right)} + (\overline{R}_k-R_F)\] Chamando \(\lambda\) de \(\frac{\sum_{i=1}^N X_i.(\overline{R}_i-R_F)}{\left(\sum_{i=1}^N X_i^2.\sigma^2_i+2.\sum_{1<i<j<N}X_i.X_j.\sigma_{i,j}\right)}\) a expressão acima se torna: \[\frac{\partial\theta}{\partial X_k}=-\lambda.\left(X_k.\sigma_k^2+\sum_{j=1,j\neq k}^NX_j.\sigma_{j,k} \right)+(\overline{R}_k-R_F)\]↩
O apostófro na notação faz referências as proporções que o mercado possui de cada ativo.↩