Índices de Inflação no Brasil

Introdução

O intuito desse post é bastante simples. Queremos coletar dados de inflação mensal através do pacote BETS e observar padrões para alguns índices no Brasil. Inicialmente, começamos carregando o pacote BETS. Na sequência, usamos a função BETSget() para fazer o download das séries desejadas. No caso, queremos o IPCA, IGP-M, IPA e IPC. O próximo passo é juntar todas as séries em uma múltipla série temporal, através do comando cbind(). Depois olhamos as últimas dez observações dos dados obtidos e transformamos o resultado em valores decimais (ao invés de %). Por fim, pedimos o plot da série.

library(BETS)

IPCA_M   <- BETSget(code = "10764")
IGPM_M   <- BETSget(code = "189")
IPA_M    <- BETSget(code = "225")
IPC_M    <- BETSget(code = "191")

Inflacao <- cbind(IPCA_M,IGPM_M,IPA_M,IPC_M)

# Últimas Observações da Série
tail(Inflacao, 10)

##          IPCA_M IGPM_M IPA_M IPC_M
## Aug 2019   0.08  -0.67 -0.90  0.17
## Sep 2019   0.09  -0.01  0.68  0.00
## Oct 2019   0.09   0.68  0.84 -0.09
## Nov 2019   0.14   0.30  1.11  0.49
## Dec 2019   1.05   2.09  2.34  0.77
## Jan 2020   0.71   0.48 -0.13  0.59
## Feb 2020   0.22  -0.04 -0.03 -0.01
## Mar 2020   0.02   1.24  2.33  0.34
## Apr 2020     NA   0.80  0.11 -0.18
## May 2020     NA   0.28    NA    NA

# Transformação em Decimal
Inflacao <- Inflacao*0.01 

plot(Inflacao, main = "Índices de Inflação Mensal",
     col = "red", xlab = "Tempo (Meses)",
     ylab = "Inflação Mensal")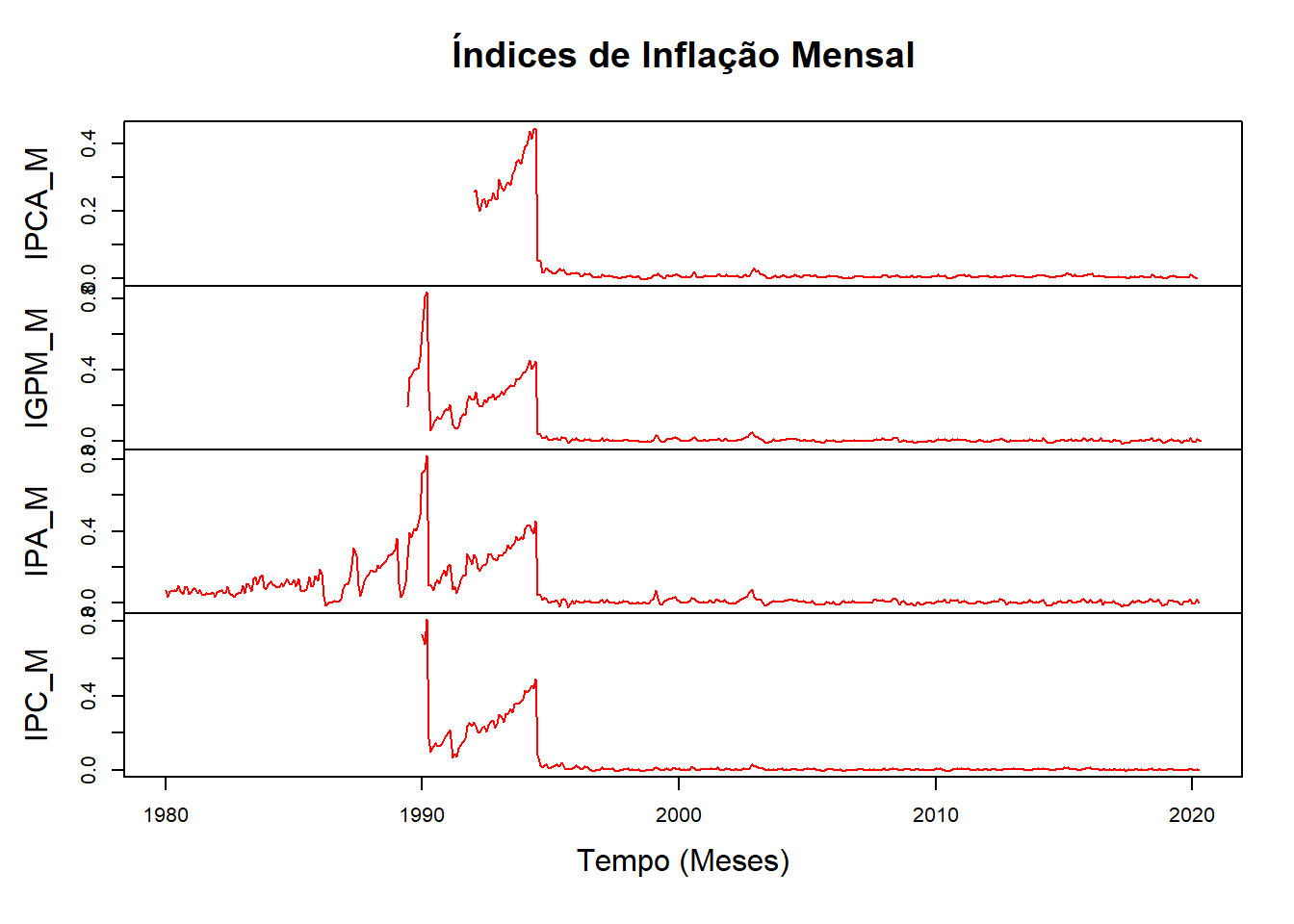

Como podemos observar, através da figura anterior, todos os índices sofrem quebra estrutural no período de implementação do plano real. Portanto, faremos agora um novo plot com recorte para dados que comecem no ano de 1995.

plot(window(Inflacao, start = c(1995,1)), 
     main = "Índices de Inflação Mensal - Pós 95",
     xlab = "Tempo (Meses)",
     ylab = "Inflação Mensal",
     col = "red")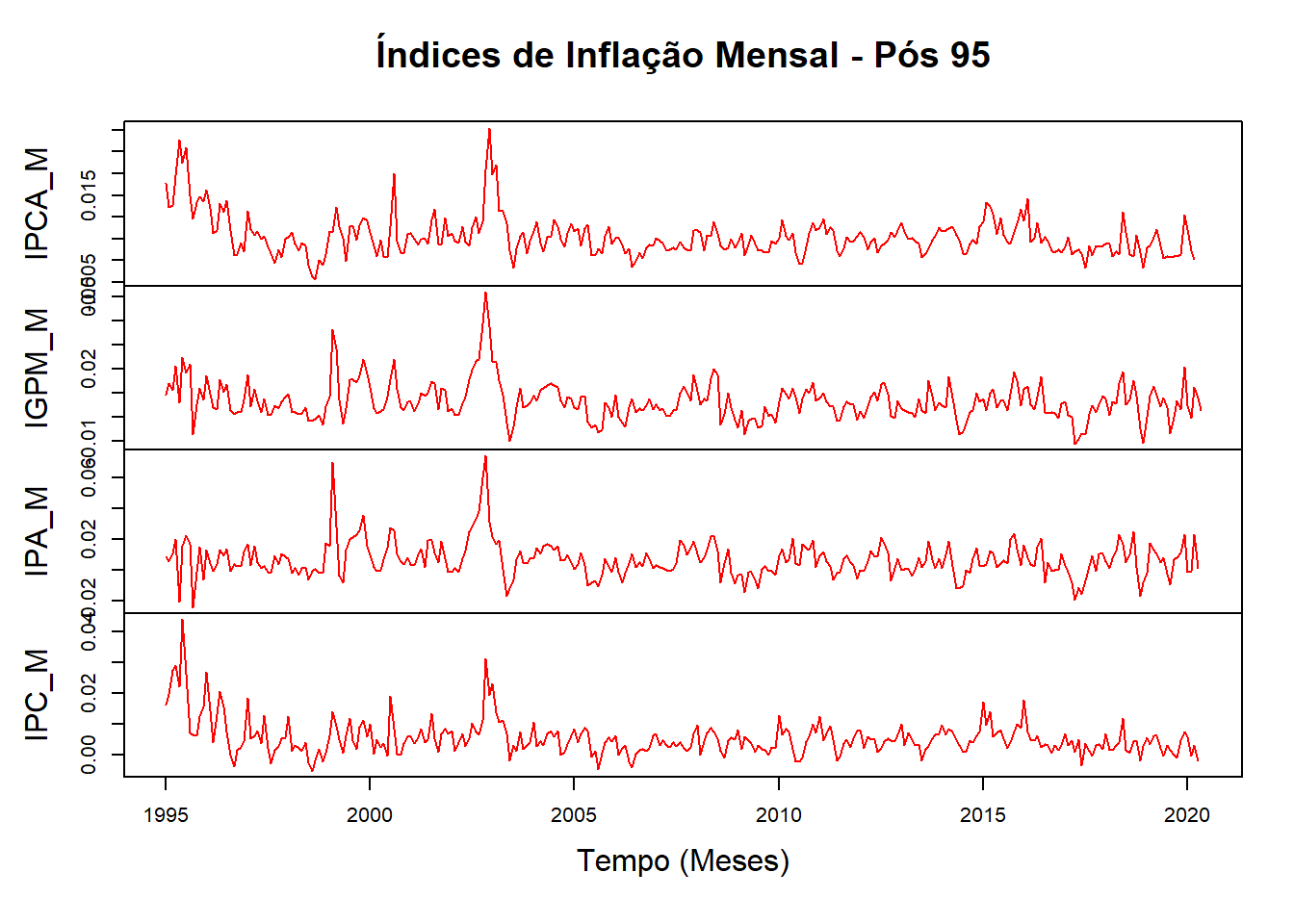

Observando a figura anterior, podemos identificar que embora não haja mais a quebra estrutural que divide o período de hiperinflação com o período atual, não podemos falar muito sobre o comportamento recente desses índices.

Dessa forma, para entender melhor, iremos agora acumulá-los para Inflação de 12 meses. Para isso, temos a seguinte equação:

\[\pi_{12 m}=\Pi_{t=1}^{t-11}(1+\pi_t)-1\] onde \(\pi_{12m}\) é a inflação de 12 meses, \(\pi_{t}\) é a inflação mensal, \(\Pi_{t=1}^{t-11}\) é o produtório do período corrente até a décima primeira defasagem.

Inflacao_12m <- ((1+Inflacao)*(1+stats::lag(Inflacao,-1))
                 *(1+stats::lag(Inflacao,-2))
                 *(1+stats::lag(Inflacao,-3))
                 *(1+stats::lag(Inflacao,-4))
                 *(1+stats::lag(Inflacao,-5))
                 *(1+stats::lag(Inflacao,-6))
                 *(1+stats::lag(Inflacao,-7))
                 *(1+stats::lag(Inflacao,-8))
                 *(1+stats::lag(Inflacao,-9))
                 *(1+stats::lag(Inflacao,-10))
                 *(1+stats::lag(Inflacao,-11)))-1

Inflacao_12m_1995 <- window(Inflacao_12m, start = c(1996,1))
colnames(Inflacao_12m_1995) <- c("IPCA", "IGP-M", "IPA", "IPC")

### Plot da Figura com Dados da Infla??o Acumulada em 12 Meses

plot(Inflacao_12m_1995, plot.type = "single", 
     col = c("red","blue","magenta","brown"),
     lwd = 2,
     main = "Inflação Acumulada em 12 Meses",
     xlab = "Tempo", 
     ylab = "Inflação Acumulada em 12 Meses",
     panel.first = grid(),
     ylim = c(-.10,0.45))
abline(h=0.00,  lty = 2, lwd = 2)
abline(h=0.045, lty = 3, lwd = 2)
legend("topleft",
       c("IPCA","IGP-M","IPA","IPC"),
       col=c("red","blue","magenta","brown"), 
       lwd = 2, cex=0.8, inset = 0.05)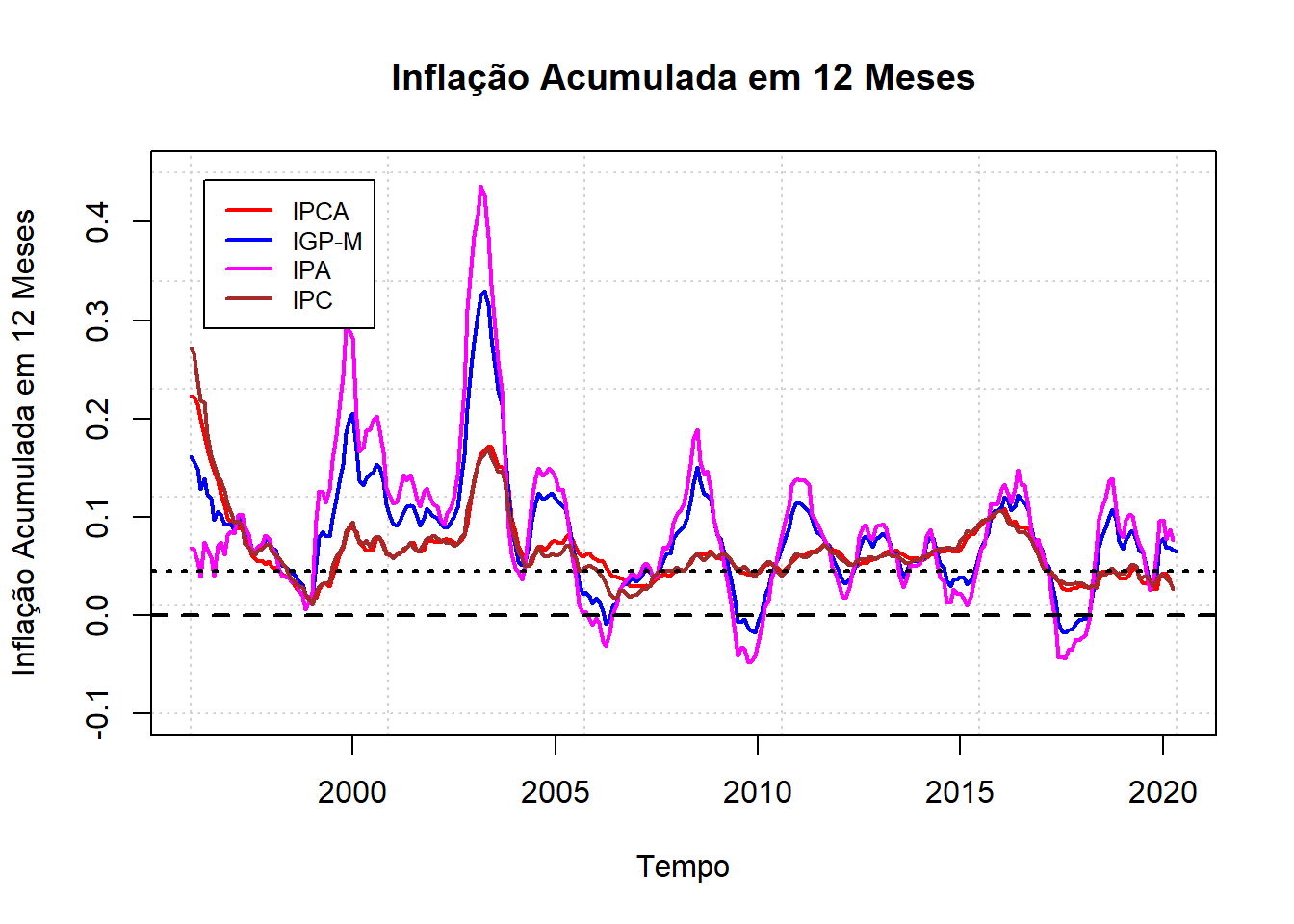

Agora se torna claro os períodos de aumento e queda da inflação pelos distintos índices. Também fica evidente que IPA e IGP-M são muito mais voláteis do que o IPCA e o IPCA. Há uma razão para isso e investigaremos em outro post. Por enquanto, segue mais algumas características descritivas das séries

summary(Inflacao_12m_1995)

##       IPCA             IGP-M               IPA                IPC         
##  Min.   :0.01656   Min.   :-0.01724   Min.   :-0.04777   Min.   :0.01049  
##  1st Qu.:0.04403   1st Qu.: 0.04396   1st Qu.: 0.03907   1st Qu.:0.04519  
##  Median :0.06063   Median : 0.07659   Median : 0.07768   Median :0.06016  
##  Mean   :0.06601   Mean   : 0.08079   Mean   : 0.08754   Mean   :0.06631  
##  3rd Qu.:0.07475   3rd Qu.: 0.10678   3rd Qu.: 0.12423   3rd Qu.:0.07372  
##  Max.   :0.22290   Max.   : 0.32951   Max.   : 0.43634   Max.   :0.27237  
##  NA's   :2                            NA's   :1          NA's   :1

### Bloxplot com os Resultados
boxplot(Inflacao_12m_1995,
        main = "Boxplot com Inflação Acumulada 12 Meses - Índices",
        col = c("red","blue","magenta","brown"),
        xlab = "Índice", ylab = "Valor da Inflação Acumulada")

Tanto a figura da inflação acumulada em 12 meses, quando a estatística descritiva e os boxplots deixam claro que apesar de todas as séries apresentarem médias próximas, a dispersão dos dados é completamente distinta.

round(tail(Inflacao_12m_1995*100,15),2)

##          IPCA IGP-M   IPA  IPC
## Mar 2019 4.18  8.28 10.30 4.90
## Apr 2019 4.71  8.66 10.11 5.20
## May 2019 4.93  7.66  8.14 5.00
## Jun 2019 3.84  6.53  7.25 3.75
## Jul 2019 3.27  6.41  6.46 3.89
## Aug 2019 3.22  4.96  4.47 4.00
## Sep 2019 3.22  3.38  2.57 3.53
## Oct 2019 2.72  3.17  3.26 2.94
## Nov 2019 2.67  3.99  6.21 3.63
## Dec 2019 3.91  7.32  9.59 4.12
## Jan 2020 4.34  7.82  9.66 4.14
## Feb 2020 4.21  6.84  7.70 3.77
## Mar 2020 3.67  6.82  8.74 3.45
## Apr 2020   NA  6.69  7.69 2.62
## May 2020   NA  6.51    NA   NA