Estimando a Estrutura a Termo da Taxa de Juros - Parte 2/3
Contextualizando
Dando continuidade ao post anterior, já discutimos o que seria a ponta longa e a ponta curta da curva de juros. Vamos agora avançar na análise da estimação da estrutura a termo (ETTJ), propriamente dita.
Sobre a ETTJ, podemos resumir o nosso problema ao seguinte: O mercado possui títulos similares com distintos prazos de maturidade frente a distintas YTM (yield to maturity ou TIR). Qual seria a melhor estimativa (ou interpolação) de curva que uniria os prazos em torno dessa linha?
Para isso, vamos começar pela análise de Modelos que podemos utilizar para esse fim.
Forma 1 - Interpolação Flat Forward Exponencial
Essa forma de interpolação consiste em tomar dois pontos no tempo em que as YTM são conhecidas. Entre esses pontos, assume-se que a taxa a termo diária permanece constante (por isso o termo flat forward, ou ainda, taxa incremental a termo constante).
Em termos matemáticos, ela pode ser definida como: \[(1+F_{wd})^{\frac{(du_2 - du_1)}{252}}=\frac{(1+i_2)^{du_2/252}}{(1+i_1)^{du_1/252}}\] onde: \(F_{wd}\) é a taxa forward (ou a termo) calculada a.a.;\(i_1\) é a YTM fixada no vencimento \(du_1\); \(i_2\) é a YTM fixada no vencimento \(du_2\), sendo \(du_2>du_1\).
Limitações: Taxa constante em todo o período e fornece apenas a suposta inclinação da ETTJ.
Forma 2 - Interpolação Linear
A interpolação linear ou aritmética é um exercício de simplemente unir o par ordenado \((du_1,i_1)\) com \((du_2,i_2)\) por um segmento de reta. Matematicamente pode ser expressa como: \[i_*=i_1+\frac{(i_2-i_1)}{(du_2-du_1)}\times(du_*-du_1)\]
Forma 3 - Interpolação por Cubic Spline
A técnica 3, conhecida como interpolação por cubic spline apresenta como vantagem uma melhor suavização da curva entre os vértices observados. Todavia, não podemos como nas técnicas anteriores fazer uso de cálculo manual.
O conceito matemático deste método consiste em gerar uma aproximação polinomial por partes. A função genérica parte da seguinte equação de terceiro grau (por isso o termo cúbico no nome!): \[f(x)=a+b.x+c.x^2+d.x^3\] Como característica dessa função, temos a geração de derivadas de 1ª e 2ª ordens. Essas nos auxiliam no cálculo dos coeficientes. Comparando essa técnica com as anteriores, temos que não há uma fórmula única de interpolação por cubic spline, uma vez que para cada conjunto de pontos, um conjunto de parâmetros \(a_i,b_i,c_i,d_i\) são estimados. Para cálcular através desse método, apresentamos o script abaixo que simula a coleta de informações de \(5\) títulos pré-fixados com datas de \(1,2,3,4\) e \(5\) anos. Taxas respectivas de \(14.5,15,16.5,16.4\) e \(16\). Utilizamos o pacote pracma que contém as funções cubicspline() e spline(). A primeira estima os parâmetros enquanto a segunda os aplica para gerar uma curva com os parâmetros estimados.
library(pracma)
Maturidade <- c(1,2,3,4,5)
YTM <- c(14.5,15,16.5,16.4,16)
pp <- cubicspline(Maturidade, YTM)
plot(Maturidade, YTM, col = "darkblue",
ylim = c(14,17),
xlab = "Prazo de Maturidade",
ylab = "Yield to Maturity (ou TIR)",
main = "ETTJ Interpolada por Cubic Spline")
lines(spline(Maturidade, YTM), col = "red", lwd =2)
grid()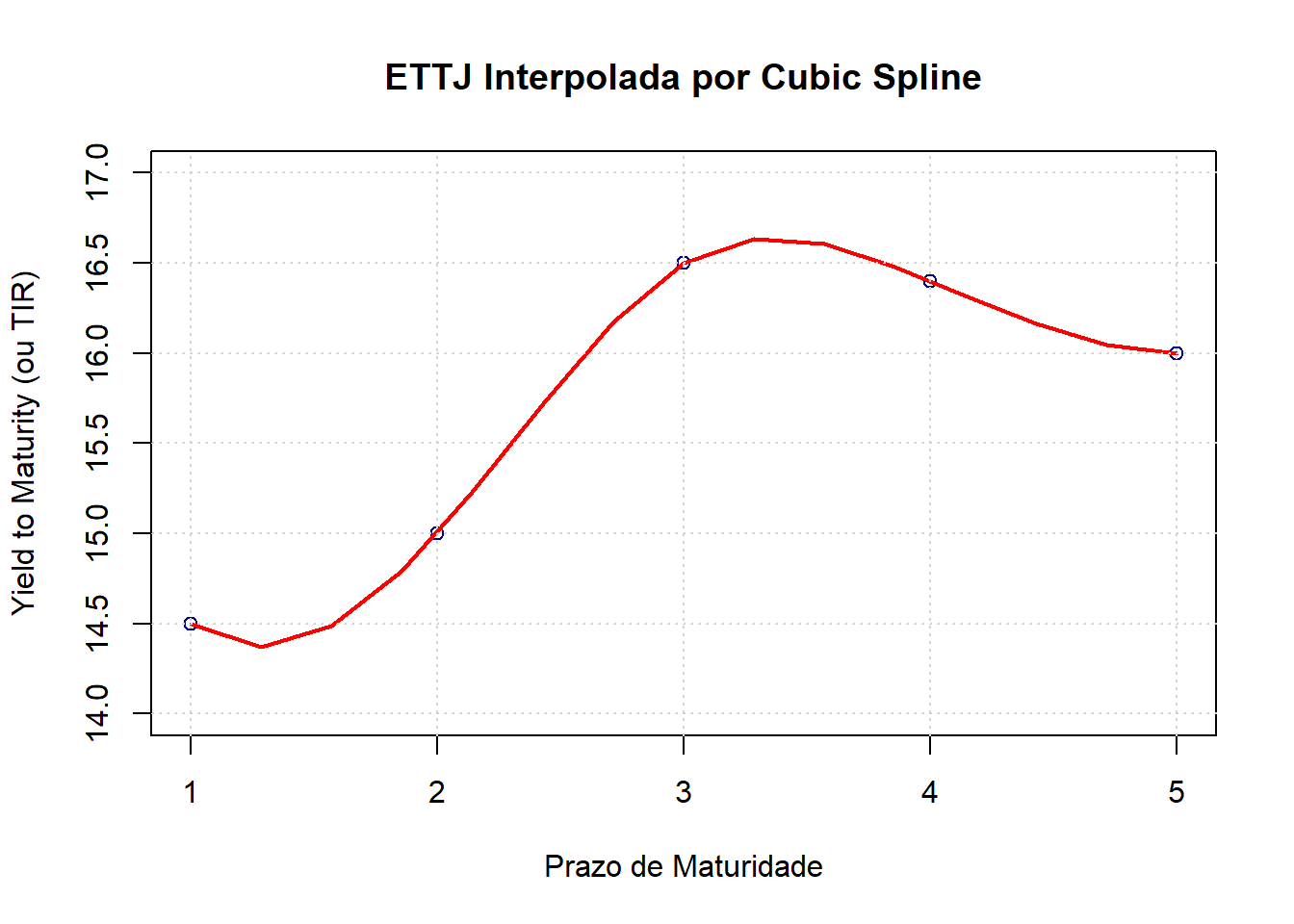
Outras Formas de Estimação da ETTJ
O Modelo de Nelson Siegel
Em 1987, Nelson e Siegel1 tiveram a ideia que ao restringir a taxa zero para que essa seja função especial da convergência para o vencimento. Deixando essa função com parâmetros livres, podemos chegar em curvas que se ajustam as condições de mercado.
A função especial que eles obtiveram possui três partes e a seguinte forma \[r(T)=\beta_0+\beta_1.\frac{(1-e^{-T/\tau})}{T/\tau}+\beta_2.\left(\frac{1-e^{-T/\tau}}{T/\tau}-e^{-T/\tau}\right)\] onde \(\beta_0,\beta_1,\beta_2\) e \(\tau\) são parâmetros constantes e \(T\) é o tempo que falta até a maturidade em unidades anuais. Especificamente, \(\beta_0\) é o parâmetro que define o nível da taxa de longo prazo. Repare que quando \(T\to\infty\), os demais termos da função também tendem a zero. O segundo parâmetro, \(\beta_1\), define o decaimento exponencial ao longo do tempo. Esse decaimento é mais lento a medida que \(\tau\) é maior. O terceiro parâmetro gera a curvatura positiva da curva (se \(\beta_2>0\)) ou curvatura negativa (se \(\beta_2<0\)).
Para entender o efeito isolado dos três componentes, desenvolvemos o seguinte script abaixo para demonstrar que a curva é a soma dos efeitos: taxa de longo prazo, decaimento e curvatura.
rm(list = ls())
beta_0 <- 0.02
beta_1 <- 0.02
beta_2 <- 0.20
tau <- 2.00
T <- seq(from = 0, to = 100, by = 0.1)
ETTJ <- beta_0 + beta_1*(1-exp(-T/tau))/(T/tau) + beta_2*((1-exp(-T/tau))/(T/tau) - exp(-T/tau))
Time_Decay <- beta_1*(1-exp(-T/tau))/(T/tau)
Hump <- beta_2*((1-exp(-T/tau))/(T/tau) - exp(-T/tau))
# Plot da Figura com a Curva Nelson Siegel
plot(T,ETTJ*100, type = "l", ylim = c(0,10), lwd = 2,
main = "ETTJ - Simulação da Curva Nelson Siegel",
ylab = "Yield to Maturity (ou TIR)",
xlab = "Prazo de Maturidade")
lines(T,Time_Decay*100, type = "l", lty = 2, lwd = 2 ,col = "red")
lines(T,Hump*100, type = "l", lty =3, lwd = 2, col = "blue")
abline(h = beta_0*100, lty = 5, col = "gray", lwd =2)
grid(nx = NULL, ny = NULL, lty = "dotted", col = "lightgray")
legend("topright",
c("Curva Nelson Seigel",
"Decaimento Temporal",
"Curvatura",
"Tx. de Longo Prazo"),
col = c("black","red","blue","gray"),
lty = c(1,2,3,5), cex = 0.8, inset = 0.05,
lwd = c(2,2,2,2))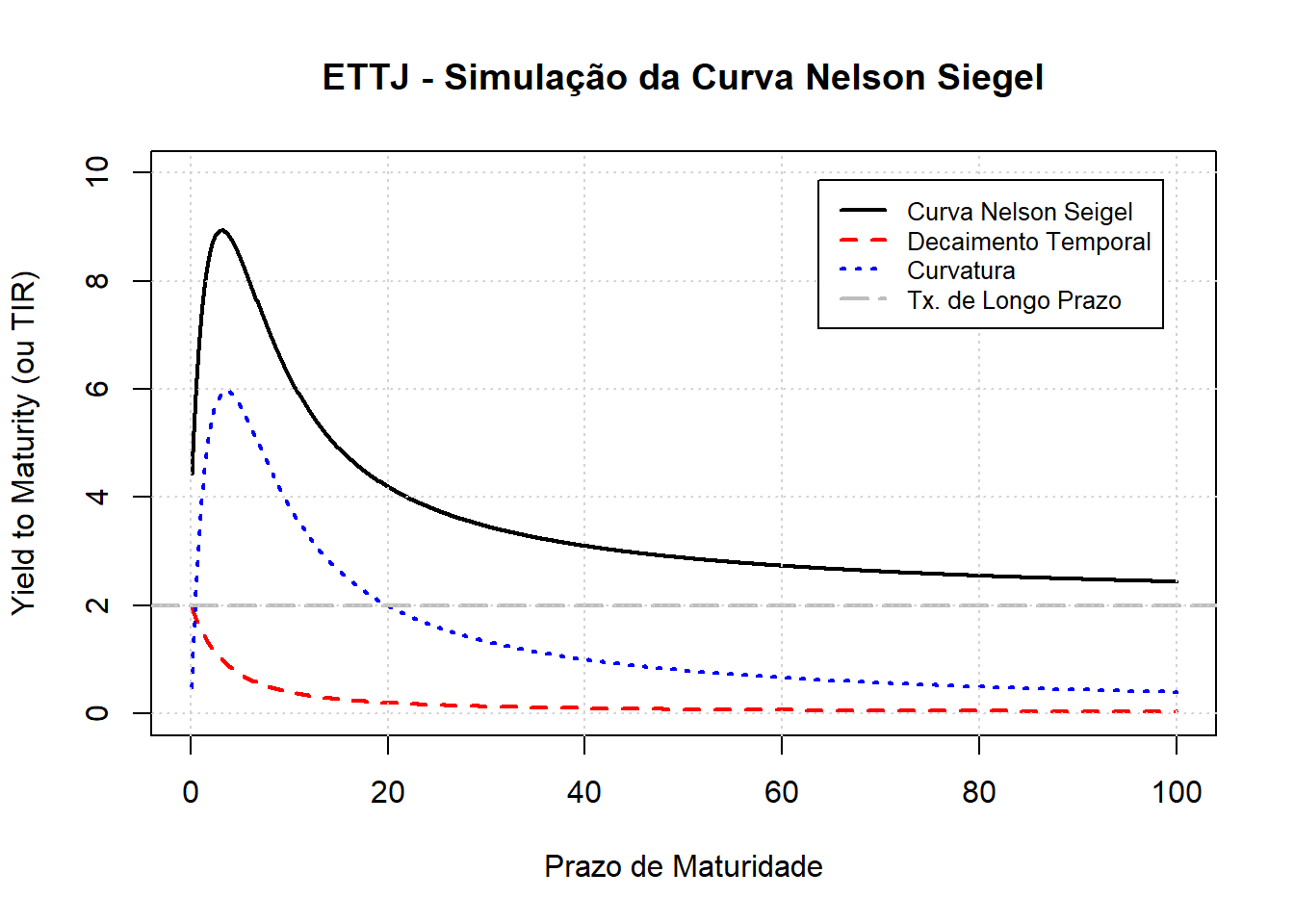
Na sequência, iremos agora utilizar o método para estimar a curva com dados reais. Apesar a forma não linear da função, ela pode ser facilmente linearizada para ser estimada por MQO. Não precisaremos fazer isso, uma vez que já existe no R um pacote específico para lidar com a estimação de NS, sendo esse o pacote YieldCurve.
Para não ser omisso, cabe aqui destacar que também há outros desdobramentos do modelo anterior. O principal é o modelo de Svensson (1994)23. Esse avança ao introduzir um novo termo, da seguinte forma: \[r(T)=\beta_0+\beta_1.\frac{(1-e^{-T/\tau})}{T/\tau}+\beta_2.\left(\frac{1-e^{-T/\tau}}{T/\tau}-e^{-T/\tau}\right)+\beta_3.\left(\frac{1-e^{-T/\tau_2}}{T/\tau_2}-e^{-T/\tau_2}\right)\] O último termo, \(\beta_3\), visa capturar o ajuste da curva a movimentos a movimentos instantâneos de juros, de maneira a permitir mais um extremo na curva. No próximo post, iremos utilizar o modelo NS para estimar dados da ETTJ para a economia brasileira.
Nelson, C., & Siegel, A. F. (1987). Parsimonious modeling of yield curves. Journal of Business, 60, 473–489.↩
Svensson, L. E. O. (1994). Estimating and interpreting forward interest rates: Sweden 1992–1994. IMF working paper, WP/94/114.↩
Svensson, L. E. O. (1996). Estimating the term structure of interest rates for monetary policy analysis. The Scandinavian Journal of Economics, 98, 163–183.↩