Estimando a Estrutura a Termo da Taxa de Juros - Parte 1/3

Last updated on Mar 5, 2020 7 min read Finanças, Macroeconomia

O Contexo

Desde os anos de 2016 para cá, temos tido uma trajetória de queda na Selic Nominal e na Taxa de Juros Real ex post. No presente momento, nos interessa responder o seguinte… Como anda, atualmente, a curvatura da Estrutura a Termo da Taxa de Juros (ETTJ)? Como se encontra a ponta curta, a ponta longa e inclinação?

Para esse propósito, vamos começar aqui contextualizando o cenário da Selic Over nos últimos 20 anos…

Taxa de Juros Real (ex ante e ex post)

Antes de começar, precisamos conceitar alguns pontos. Temos na literatura a definição de duas variáveis relacionadas ao cálculo da taxa de juros real, sendo elas a taxa ex ante e a taxa ex post. Podemos definí-las como:

Taxa de juros real ex ante: \[r_{ex\ ante}=(1+{i_t}_{selic\ over})/(1+E_{t-1}(\pi_{t})) -1\]

Taxa de juros real ex post: \[r_{ex\ post}=(1+{i_t}_{selic\ over})/(1+\pi_{t}) -1\]

Onde \(r_{ex\ ante}\) é a taxa de juros real ex ante; \(r_{ex\ post}\) é a taxa de juros real ex post; \(\pi_{t}\) é a inflação obtida pelo IPCA; \(E_{t-1}(\pi_{t})\) é a expectativa de inflação coletada pelo boletim focus (proxy).

Script para obtenção e tratamento:

O script faz uso do pacote BETS ou Brazilian Economic Time Series, criado pelos pesquisadores da IBRE-FVG. Atualmente, o pacote alimenta um banco de dados com mais de 18 mil séries temporais, as quais podemos acessar via funções BETSsearch() e BETSget(). A primeira é utilizada para conhecer as séries existentes no banco de dados e a segunda é para fazer o seu download.

library(BETS)

rm(list=ls())

Selic_M <- window(BETSget(code = "4390" )*0.01, start = c(1995,1))
IPCA_M  <- window(BETSget(code = "10764")*0.01, start = c(1995,1))

Selic_real_ex_post <- ((1+Selic_M)/(1+IPCA_M) -1)

plot(Selic_real_ex_post, main = "Selic Real ex post",
                         ylab = "Juros Real",
                         xlab = "Tempo")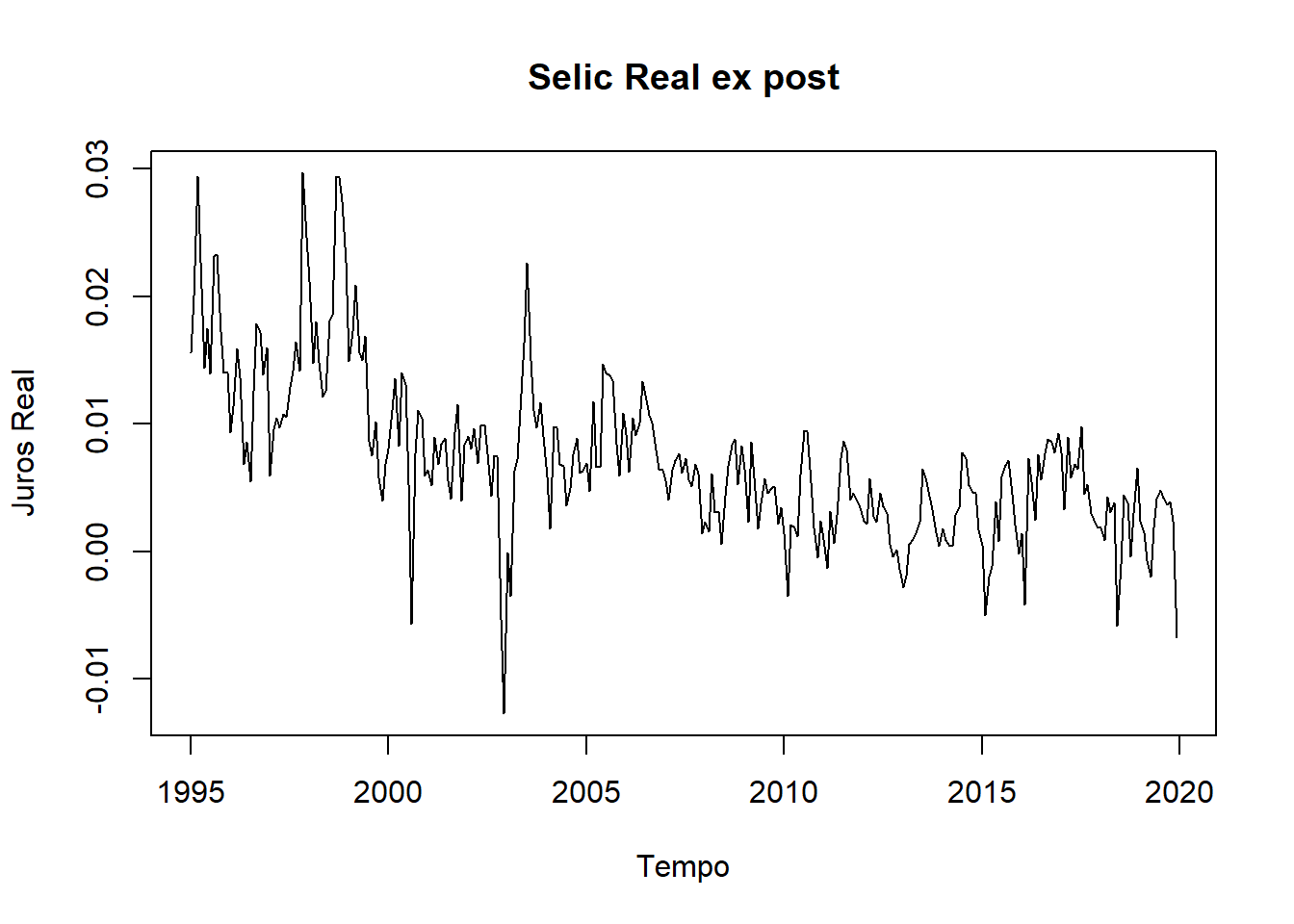

Todavia, a análise da trajetória da taxa de juros, seja ela nominal ou real, em termos mensais não nos evidencia comportamentos claros. Para esse fim, iremos acumulá-la em 12 meses, fazendo uso da seguinte equação:

\[r_{12 \ meses}=[\prod_{t=1}^{t-11}(1+r_t)]-1\] Ou seja, aplicamos o produtório na taxa real de juros do período atual até a 11ª defasagem. Sobre o valor obtido, retiramos 1. O resultado obtido na trajetória acumulada mostra a tendência de queda que a Selic real tem tido históricamente. A maior redução ocorre no período pós 99, período esse que marca a mudança do regime de bandas cambiais para a instituição do regime de metas de inflação (RMI) no Brasil. No período, a média do juros real foi de 8,96% a.a. Recentemente, houve dois “flertes” da taxa de juros real com o mínimo histórico. O primeiro se deu em Junho de 2013, no qual o acumulado do juros real ex post bateu 0,6% a.a. O segundo se deu em Maio de 2019, com o valor alcançado no acumulado de 12 meses de 1,35% a.a. No última valor observado dos dados, temos a taxa acumulada em 1,95% a.a. O cenário mundial não diverge desse. Temos, em alguns casos, a prática de juros real negativo e cornetas apontando para maior afrouxamento monetário coordenado mundo a fora!

Selic_real_12 <- ((1+Selic_real_ex_post)*
                  (1+stats::lag(Selic_real_ex_post,-1))*
                  (1+stats::lag(Selic_real_ex_post,-2))*
                  (1+stats::lag(Selic_real_ex_post,-3))*
                  (1+stats::lag(Selic_real_ex_post,-4))*
                  (1+stats::lag(Selic_real_ex_post,-5))*
                  (1+stats::lag(Selic_real_ex_post,-6))*
                  (1+stats::lag(Selic_real_ex_post,-7))*
                  (1+stats::lag(Selic_real_ex_post,-8))*
                  (1+stats::lag(Selic_real_ex_post,-9))*
                  (1+stats::lag(Selic_real_ex_post,-10))*
                  (1+stats::lag(Selic_real_ex_post,-11))-1)

plot(Selic_real_12*100, main = "Selic Real ex post - Acumulada 12 Meses",
                        ylab = "Juros Real (%)",
                        xlab = "Tempo", 
                        lwd = 2, 
                        col = "red")
grid(nx = NULL, ny = NULL, col = "lightgray", lty = "dotted")
abline(h = mean(Selic_real_12)*100, lty = 2, lwd = 2)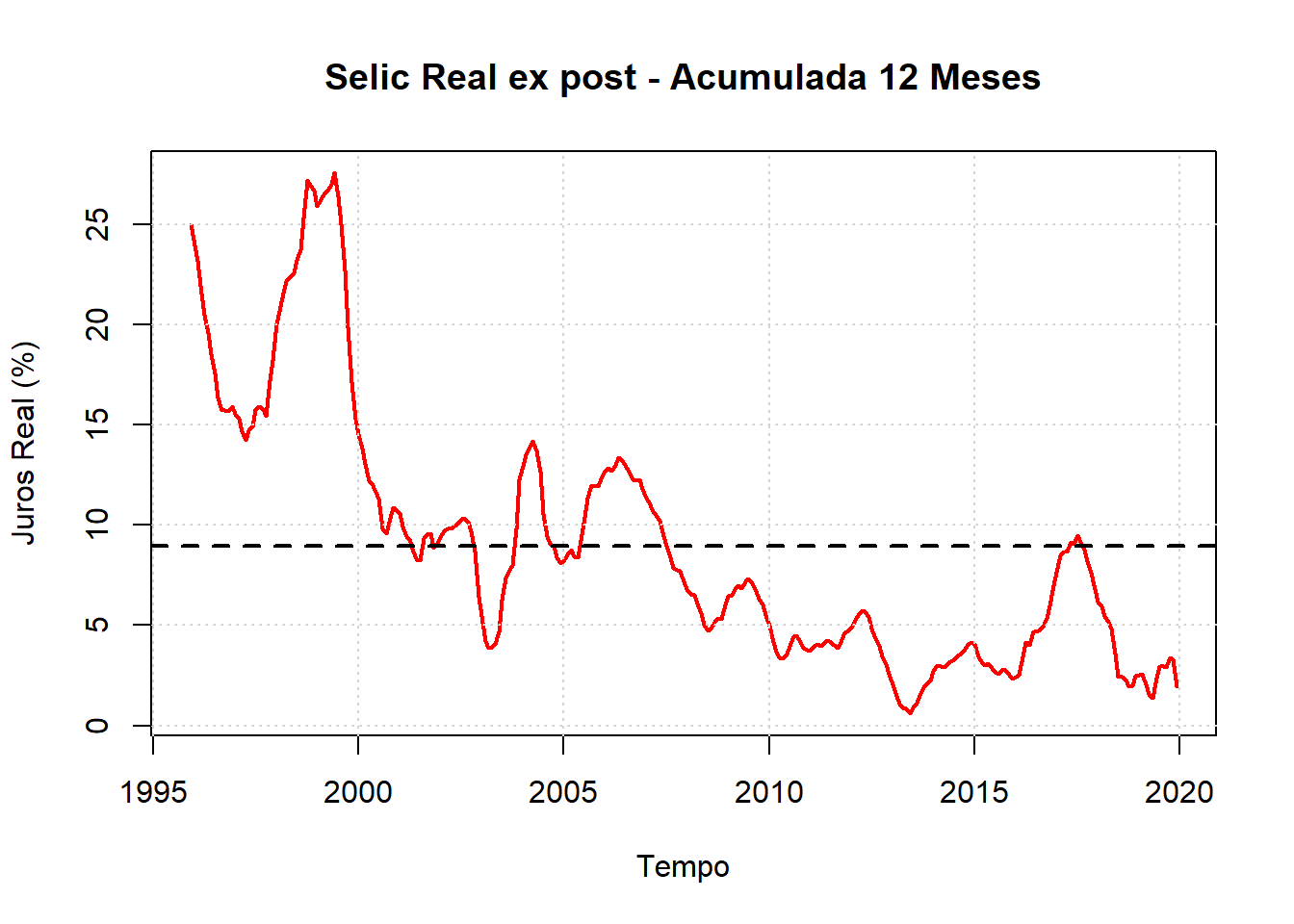

A Ponta Longa da Taxa de Juros

Isso posto, nos interessa agora abordar uma outra questão relacionada com a taxa de juros! Qual o formato da curva nos dias atuais… para isso, precisaremos mudar nossa base de dados. Ao invés de trabalhar com Selic Over, vamos agora utilizar as taxas obtidas dos títulos públicos pré-fixados (LTN) e pós-fixados (NTN-B).

As LTN’s são títulos pré-fixados do tesouro sem pagamento de cupom. Elas nos possibilitam verificar a Yield to Maturity (YTM) frente ao vencimento do Título. O único problema desse título é que não possui prazo tão longo, nos impossibilitando de inferir com precisão a ponta longa da curva.

As NTN-Bs são títulos pós-fixados “híbridos”. Chamamos de híbridos porque esses são fixados em preço (remuneram o IPCA no período) mais uma taxa pré-fixada pré-acordada. Na prática, o título é uma proxy para analisar a taxa de juros real ex ante de médio e longo prazo, uma vez que a maturidade dos títulos é bem mais longa do que das LTN’s.

Nesse primeiro post, iremos tratar de avaliar o valor da taxa de juros longa. Para isso, fazeremos o download e tratamento dos títulos NTN-B’s com prazo para 2050 (30 anos a frente da data atual). Para facilitar nossa vida, faremos uso do pacote GetTDData, elaborado pelo professor Marcelo Perlin, disponivel no CRAN para download.

O pacote é uma mão na roda! A alternativa seria entrar no site do Tesouro Direto https://sisweb.tesouro.gov.br/apex/f?p=2031:2:0:::: baixar todas as planilhas, agrupar os dados e tratar. Usaremos também o pacote xts que permite trabalhar com séries temporais irregulares (tais como ativos cotados em dias úteis) e o famoso pacote gráfico highcharter

#install.packages("GetTDData")

library(GetTDData)
library(xts)
library(highcharter)
library(widgetframe)


ntnb   <- download.TD.data('NTN-B')

## 
## Downloading html page (attempt = 1|10)
## Downloading file TD Files/NTN-B_2020.xls (1-18) Downloading...
## Downloading file TD Files/NTN-B_2019.xls (2-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2018.xls (3-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2017.xls (4-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2016.xls (5-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2015.xls (6-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2014.xls (7-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2013.xls (8-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2012.xls (9-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2011.xls (10-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2010.xls (11-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2009.xls (12-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2008.xls (13-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2007.xls (14-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2006.xls (15-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2005.xls (16-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2004.xls (17-18) Found file in folder, skipping it.
## Downloading file TD Files/NTN-B_2003.xls (18-18) Found file in folder, skipping it.

ntnb50 <- read.TD.files(dl.folder = 'TD Files', 
                        maturity = '150850')

## 
## Reading xls data and saving to data.frame
##  Reading File = TD Files/NTN-B_2003.xls
##     Cant find maturities in file  TD Files/NTN-B_2003.xls
##  Reading File = TD Files/NTN-B_2004.xls
##     Cant find maturities in file  TD Files/NTN-B_2004.xls
##  Reading File = TD Files/NTN-B_2005.xls
##     Cant find maturities in file  TD Files/NTN-B_2005.xls
##  Reading File = TD Files/NTN-B_2006.xls
##     Cant find maturities in file  TD Files/NTN-B_2006.xls
##  Reading File = TD Files/NTN-B_2007.xls
##     Cant find maturities in file  TD Files/NTN-B_2007.xls
##  Reading File = TD Files/NTN-B_2008.xls
##     Cant find maturities in file  TD Files/NTN-B_2008.xls
##  Reading File = TD Files/NTN-B_2009.xls
##     Cant find maturities in file  TD Files/NTN-B_2009.xls
##  Reading File = TD Files/NTN-B_2010.xls
##     Cant find maturities in file  TD Files/NTN-B_2010.xls
##  Reading File = TD Files/NTN-B_2011.xls
##     Cant find maturities in file  TD Files/NTN-B_2011.xls
##  Reading File = TD Files/NTN-B_2012.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2013.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2014.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2015.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2016.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2017.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2018.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2019.xls
##     Reading Sheet NTN-B 150850
##  Reading File = TD Files/NTN-B_2020.xls
##     Reading Sheet NTN-B 150850

### Transformando o Data.frame da NTN-B 2050 em XTS
dates50          <- as.Date(ntnb50$ref.date, format = "%YY/%m/%d") 
ntnb50_ytm_xts   <- as.xts(ntnb50[,2]*100, order.by = dates50)
ntnb50_preco_xts <- as.xts(ntnb50[,3], order.by = dates50)

### Plot da YTM e Preço da NTN-B 2050 
frameWidget(hchart(ntnb50_ytm_xts, color = "red", 
                   name = "Taxa de Juros Pré-fixada da NTN-B") %>%
                   hc_yAxis_multiples(
                   list(lineWidth = 3),
                   list(showLastLabel = FALSE, opposite = TRUE)) %>%
                   hc_add_series(ntnb50_preco_xts, color = "black", 
                            name = "Preço da NTN-B", yAxis = 1) %>%
                   hc_title(text = "NTN-B 2050 - Preço e YTM", margin = 10, 
                       style = list(fontSize= "14px")) %>%
                   hc_subtitle(text = "Dados Diários: Mai/12 a Mar/20"))

Assim, pode-se ver com uma lupa o que está ocorrendo com a ponta longa da ETTJ. Todavia, nos resta entender o que anda acontecendo entre essas pontas… isso é um assunto para o próximo post!

Macroeconomia Finanças Estrutura a Termo da Taxa de Juros

Júlio Fernando Costa Santos

Professor of Economics

My research interests include Finance, Macroeconomics and Econometric techniques.