Contribuição Marginal ao Risco

A Contribuição Marginal ao Risco de um Portfólio

Um assunto acerca da teoria do portfólio que é de interesse dos investidores é como medir o quanto de risco que um ativo individualmente proporciona para o nosso portfólio. A Moderna Teoria de Carteiras (MTP) postula que: a) O retorno esperado de um portfólio é a média ponderada dos retornos esperados ponderada pela share dos ativos que compõem o portfólio. b) O risco de um portfólio não é a média ponderada dos riscos individuais das ações. É necessário capturar a dependência existente entre as séries.

Formalmente, temos que o retorno da esperado da carteira é dado por:

\(R_p=\sum_{i = 1}^{n} a_i.E(R_i)=a_1.E(R_1)+a_2.E(R_2)+...+a_n.E(R_n)\)

Enquanto que a variância de um portfólio é dado por:

\(\sigma^2_{Port}=\sum_{i = 1}^{n} a_i^2.\sigma_i^2+2.\sum_{1 \le i \le j \le n}a_i.a_j.\sigma_{ij}\)

A equação acima mostra que a variância da carteira, \(\sigma^2_{Port}\), depende não apenas das variâncias individuais dos ativos, \(\sigma^2_i\), mas também da estrutura de covariância de um ativo com os demais ativos, dado por \(\sigma_{ij}\ \forall\ i_\neq j\). Repare que podemos também representar fazendo uso da correlação entre os ativos, \(\rho_{ij}\), e os desvios-padrão individuais, \(\sigma_i\). Sabendo que a covariância é a correlação multiplicada pelos desvios, ou seja, \(\sigma_{ij}=\rho_{ij}.\sigma_i.\sigma_j\) temos que a equação da variância do portfólio se torna:

\(\sigma^2_{Port}=\sum_{i = 1}^{n} a_i^2.\sigma_i^2+2.\sum_{1 \le i \le j \le n}a_i.a_j.\rho_{ij}.\sigma_i.\sigma_j\)

library(PerformanceAnalytics)
library(quantmod)
library(xts)
library(unikn)
library(corrplot)

Data_inicial <- "2010-01-01"
Data_final   <- Sys.Date()
Data_final

## [1] "2020-01-26"

Baixando dados de algumas Ações da B3

Segue a parte de coleta e organização de dados.

data.ABCB4 <- getSymbols("ABCB4.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.CVCB3 <- getSymbols("CVCB3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.ENBR3 <- getSymbols("ENBR3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.ITSA4 <- getSymbols("ITSA4.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.MDIA3 <- getSymbols("MDIA3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.MYPK3 <- getSymbols("MYPK3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.KLBN4 <- getSymbols("KLBN4.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.WIZS3 <- getSymbols("WIZS3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.PMAM3 <- getSymbols("PMAM3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.SUZB3 <- getSymbols("SUZB3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.SHUL4 <- getSymbols("SHUL4.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)
data.RLOG3 <- getSymbols("RLOG3.SA", from = Data_inicial, to = Data_final, auto.assign = FALSE)

Precos <- cbind(data.ABCB4$ABCB4.SA.Adjusted,
                data.CVCB3$CVCB3.SA.Adjusted,
                data.ENBR3$ENBR3.SA.Adjusted,
                data.ITSA4$ITSA4.SA.Adjusted,
                data.MDIA3$MDIA3.SA.Adjusted,
                data.MYPK3$MYPK3.SA.Adjusted,
                data.KLBN4$KLBN4.SA.Adjusted,
                data.WIZS3$WIZS3.SA.Adjusted,
                data.PMAM3$PMAM3.SA.Adjusted,
                data.SUZB3$SUZB3.SA.Adjusted,
                data.RLOG3$RLOG3.SA.Adjusted,
                data.SHUL4$SHUL4.SA.Adjusted)

colnames(Precos) <- c("ABCB3","CVCB3","ENBR3","ITSA4","MDIA3",
                      "MYPK3","KLBN4","WIZS3","PMAM3","SUZB3","RLOG3","SHUL4")

Precos_Mensais <- to.monthly(Precos, indexAt = "first", OHLC = FALSE)
plot(Precos_Mensais)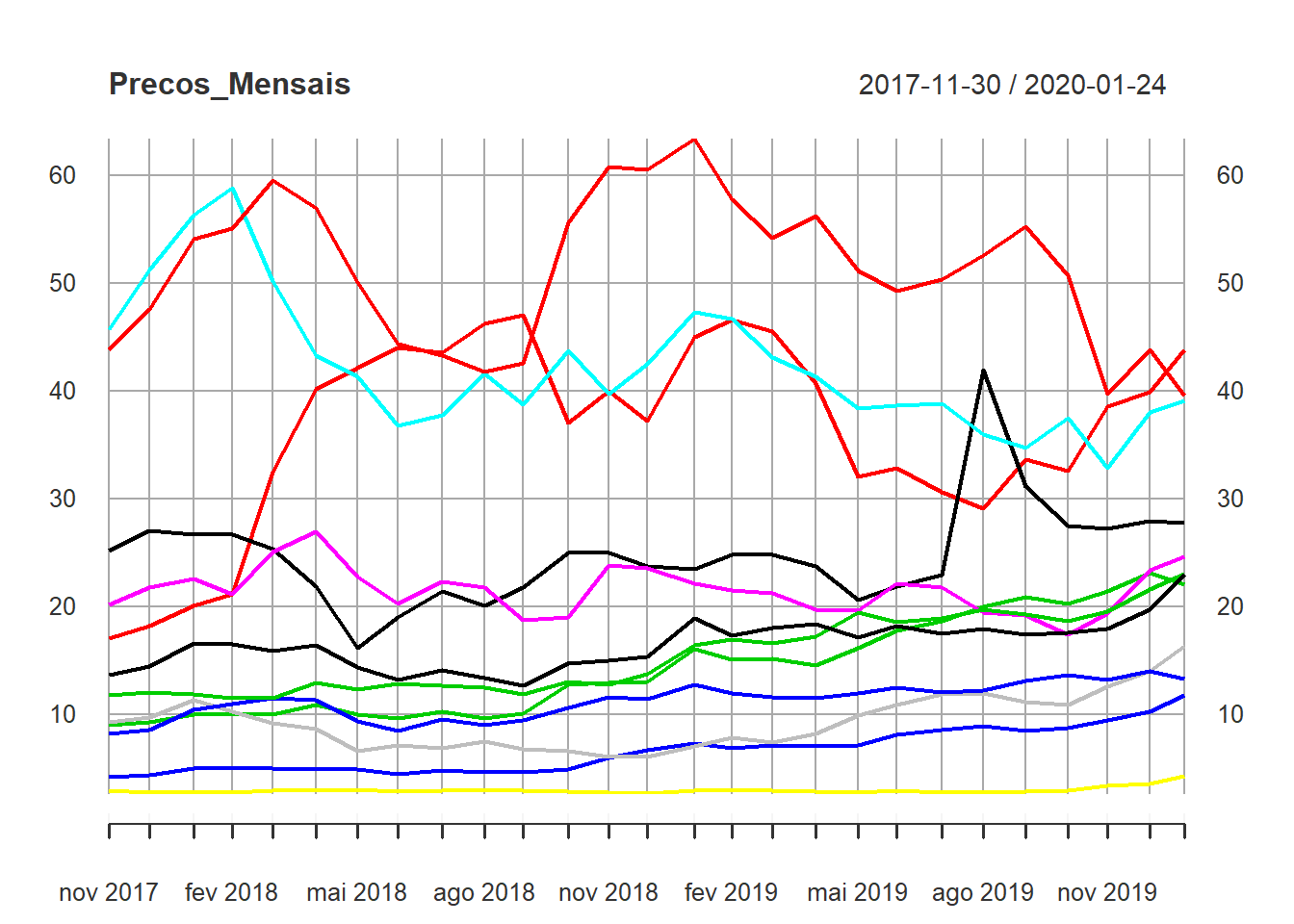

No quadro anterior, utilizamos o pacote “quantmod” para obter do YahooFinance as cotações de preço atualizadas das ações que compoem o nosso portfólio hipotético. Na sequência, iremos transformar as cotações diárias em retorno através da função “Return.calculate” que faz parte do pacote “PerformanceAnalytics”. O método de cálculo é o usual, \(\Delta P_t/P_{t-1}=P_t/P_{t-1}-1\). A partir dos valores obtidos de retorno diário, plota-se a figura .

Retornos   <- na.omit(Return.calculate(Precos))

n <- ncol(Precos)
my_pal <- usecol(pal_unikn,n = n)

plot.new()
ts.plot(Retornos*100, col = my_pal, ylim = c(-15,40),
        main = "Retorno diário das Ações",
        ylab = "Variação %", xlab = "Tempo")
legend("topleft", legend = colnames(Precos), 
       col = my_pal, lwd = 3, horiz = F, cex = 0.6)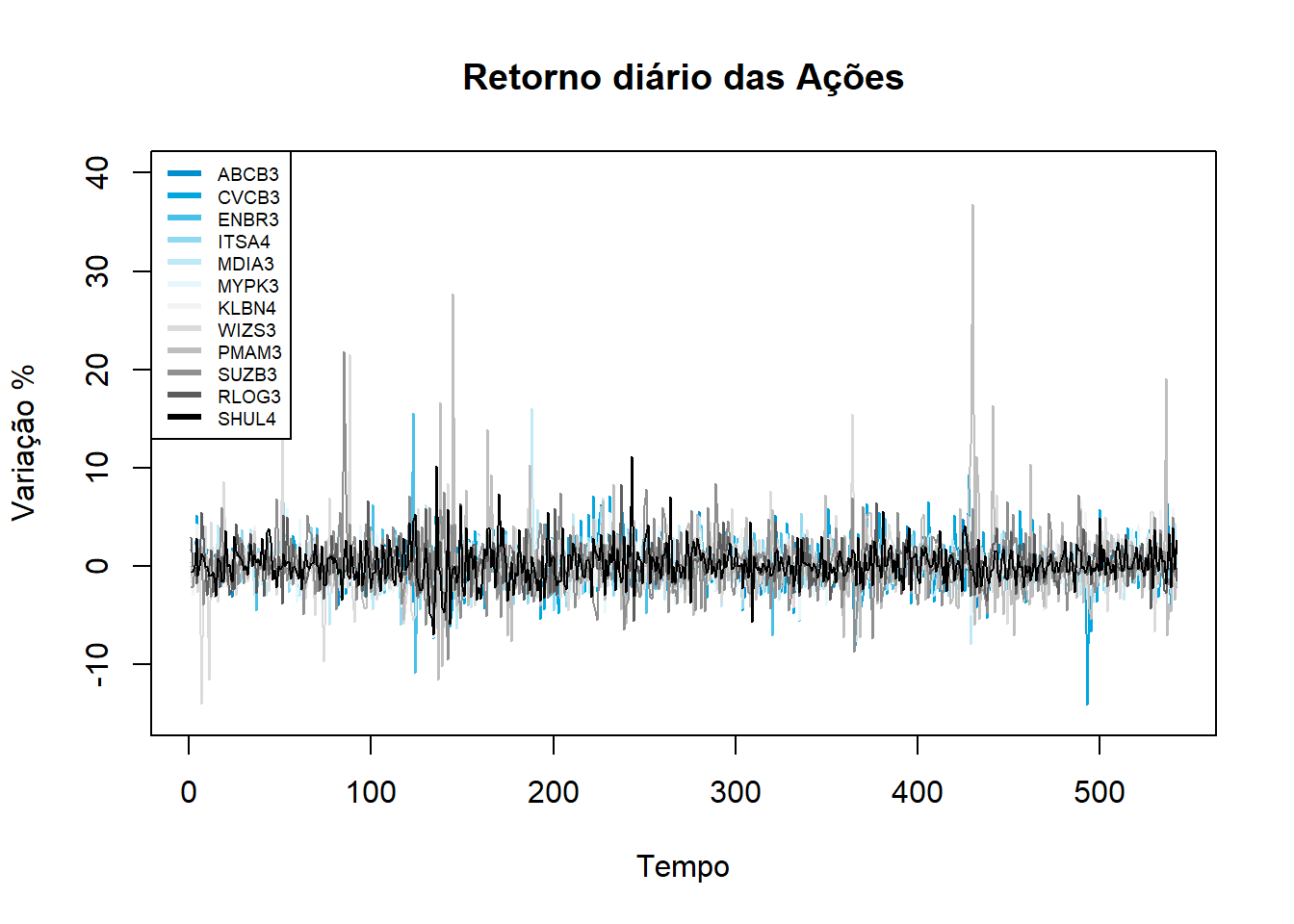

Sabendo então a trajetória de preços e a a série de retorno diários, podemos avaliar a estrutura de correlação entre o retorno dos ativos que fazem parte do portfólio.

corr_matriz <- cor(Retornos,Retornos)

col<- colorRampPalette(c("red", "white", "blue"))(20)
corrplot(corr_matriz, method="color", 
         type="upper", order="hclust", 
         tl.col="brown", tl.srt=45, 
         col=col,  addCoef.col = "black")

Neste momento iremos calcular a contribuição marginal que cada ação traz para a volatilidade do Portfólio tendo em vista que aplicaremos iguais fatias do capital em cada ação, ou seja, o peso por ação será de \(1/n\).

w <- rep(1/n,n)
cov_matriz <- cov(Retornos)

sd_portfolio          <- sqrt(t(w) %*% cov_matriz %*% w)
contribuicao_marginal <- w %*% cov_matriz / sd_portfolio[1, 1]

contribuicao_componentes <- contribuicao_marginal * w 
soma_componentes         <- rowSums(contribuicao_componentes)
percentual_componentes   <- contribuicao_componentes / sd_portfolio[1, 1]

### Plot das Barras de Contribuição com Pesos Reais
barplot(percentual_componentes[1:n], 
        col = my_pal, 
        legend.text = colnames(Precos),
        horiz=TRUE, 
        cex.names=0.8, 
        xlim = c(0, 0.30),
        main = "Contribuição Percentual de Risco (Shares 1/n)")
abline(v = mean(percentual_componentes), lty = 2)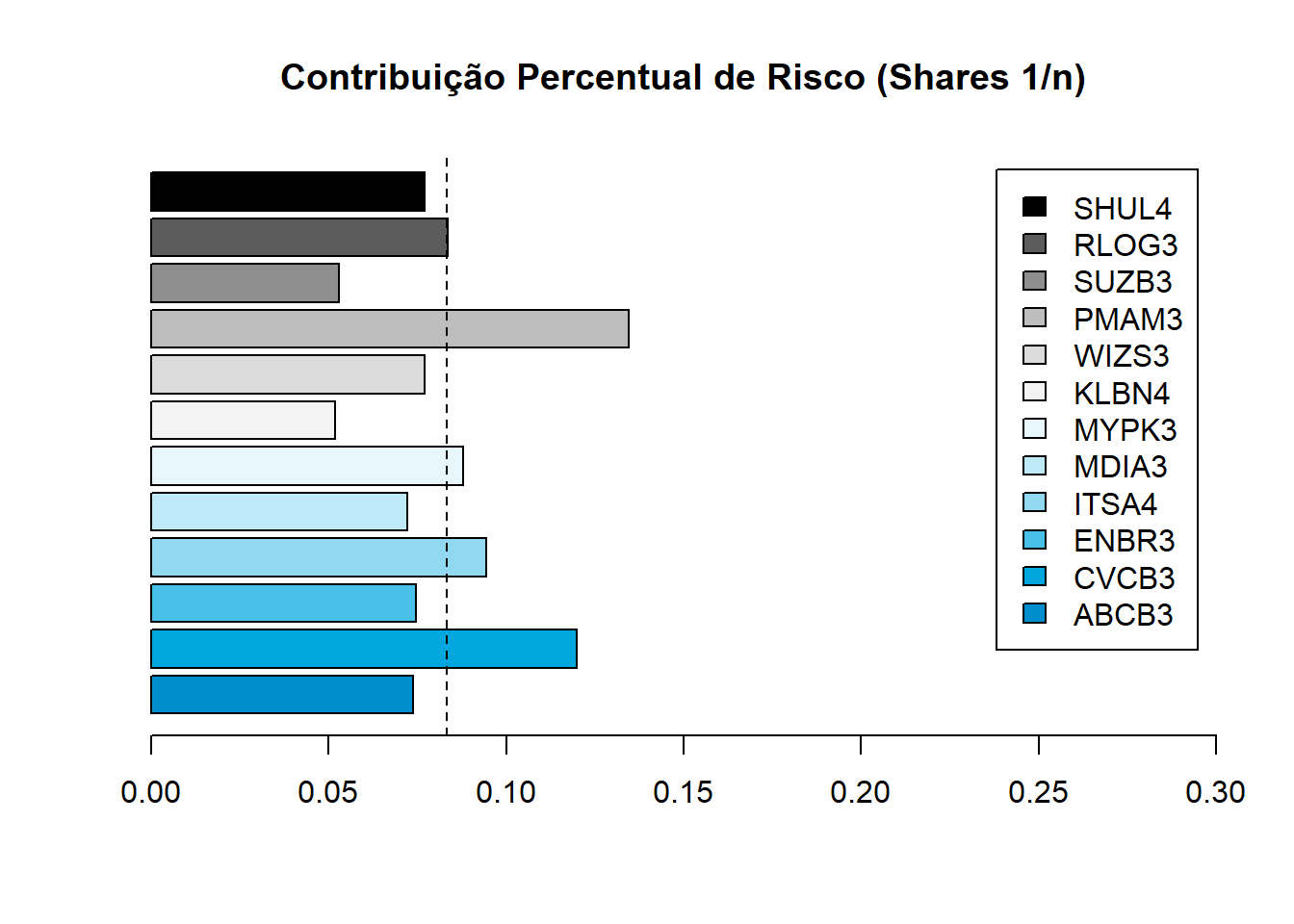

A utilização de uma carteira fictícia com shares na proporção de \(1/n\) é útil no sentido de avaliar o quando cada ativo individualmente traria de risco para carteira se fosse alocado em igual proporção com os demais. Essa informação é importante qualitativamente por informar quais são os ativos que estariam abaixo da média (portanto menos voláteis e com fraca fraca correlação com os demais ativos). Todavia, o cálculo anterior faz uso de uma estrutura com pesos iguais (shares) entre os ativos. Iremos agora simular uma aplicação real, para calcular pesos diferentes. Para isso, iremos informar o quanto possuímos de quantidade de ações, calcularemos o valor financeiro e avaliaremos o share como sendo o percentual financeiro do total que está alocado naquele ativo.

Qt_Acoes   <- c(140,115,300,360,200,300,3900,473,100,200,446,500)
Financeiro <- t(t(data.frame(Precos))*Qt_Acoes)
Pesos_W    <- Financeiro/rowSums(Financeiro, na.rm = TRUE)

sd_portfolio          <- sqrt(t(Pesos_W[nrow(Pesos_W),]) %*% cov_matriz %*% Pesos_W[nrow(Pesos_W),])
contribuicao_marginal <- Pesos_W[nrow(Pesos_W),] %*% cov_matriz / sd_portfolio[1, 1]

contribuicao_componentes <- contribuicao_marginal * Pesos_W[nrow(Pesos_W),] 
soma_componentes         <- rowSums(contribuicao_componentes)
percentual_componentes   <- contribuicao_componentes / sd_portfolio[1, 1]

### Plot das Barras de Contribuição com Pesos Reais
barplot(percentual_componentes[1:n], 
        col = my_pal, 
        legend.text = colnames(Precos),
        horiz=TRUE, 
        cex.names=0.8, 
        xlim = c(0, 0.30),
        main = "Contribuição Percentual de Risco (Shares Real)")
abline(v = mean(percentual_componentes), lty = 2)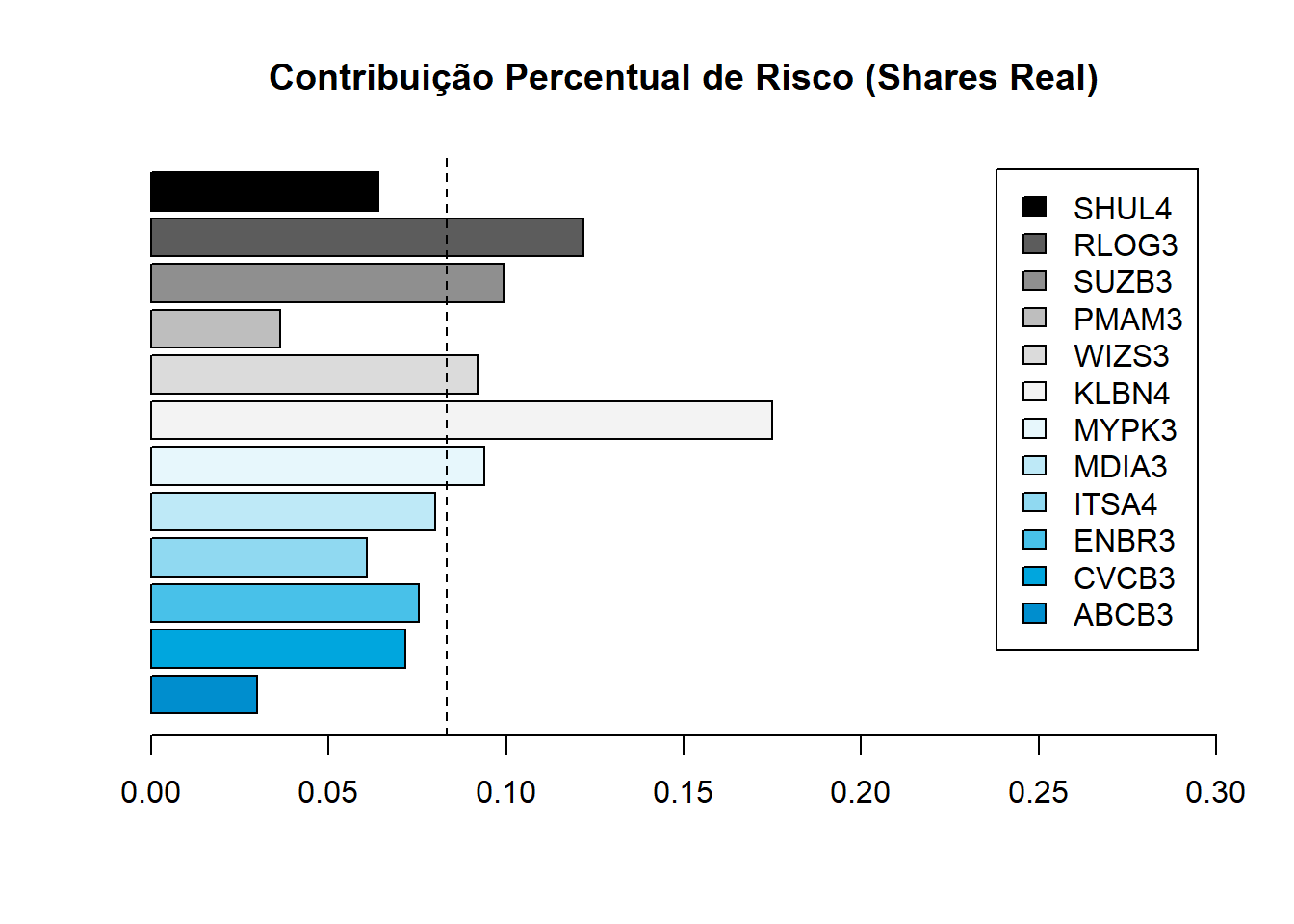

Ao fim, tendo ponderado o quanto há de cada ativo pelo seu devido peso, chegamos a conclusão que embora individualmente a ação de KLBN3 seja de menor risco para a carteira, neste momento com peso maior ela está puxando o risco para acima da média (linha tracejada), bem como RLOG3 e SUZB3. Novas aplicações (aportes) devem ser feitos no sentido de rebalancear para elevar o share ações mais abaixo da média, tais como ABCB3 e SHUL4. PMAM3 é um caso de ativo que por construção, deseja-se manter baixo share na carteira.