A Diversificação com Dois e Três Ativos

Harry M. Markowitz - Prêmio Nobel (1990)
A Análise de Risco e Retorno de um Portfólio com 2 Ativos
Uma forma intuitiva de aprender o ganho existente na diversificação de um portfólio começa ao investigar o que ocorre com uma carteira com 2 ativos e posteriormente em uma carteira com 3 ativos.
Um primeiro ponto precisa ser destacado tanto para o retorno de uma carteira quanto para a sua mensuração de risco.
- Uma carteira com 2 ativos tem como retorno esperado a média ponderada dos retornos individuais esperados ponderada pelos devidos shares de cada ativo. De maneira mais formal, temos:
\(E(R_{P})=a_1.E(R_1)+(1-a_1).E(R_2)\) sendo \(a_2=(1-a_1)\)
- Uma carteira com 2 ativos tem na composição da sua variância a variância individual dos ativos e a dependência entre eles, dada pela covariância. De maneira mais formal, temos:
\(\sigma_{P}^2=a_1^2.\sigma^2_2+(1-a_1)^2.\sigma^2_2+2.a_1.(1-a_1).\sigma_{1,2}\) sendo \(\sigma_{1,2}=\rho_{1,2}.\sigma_1.\sigma_2\)
Onde \(\sigma_{1,2}\) é a covariância entre o retorno ativo 1 e o ativo 2, \(\rho_{1,2}\) é a correlação. Os termos \(\sigma_1^2\), \(\sigma_2^2\), \(\sigma_1\) e \(\sigma_2\) são as variâncias e desvio-padrões dos retornos dos respectivos ativos 1 e 2.
Repare que sobre a análise da variância do portfólio, três possíveis casos extremos podem surgir:
- Caso 1: Correlação Positiva Perfeita, \(\rho_{1,2}=1\)
- Caso 2: Ausência de Correlação, \(\rho_{1,2}=0\)
- Caso 3: Correlação Negativa Perfeita, \(\rho_{1,2}=-1\)
Vamos agora, na sequência, detalhar cada um desses:
Caso 1: Correlação Positiva Perfeita, \(\rho_{1,2}=1\)
Fazendo uso da equação da variância do portfólio e da correlação igual a um, temos que:
\(\sigma_{P}^2=a_1^2.\sigma^2_2+(1-a_1)^2.\sigma^2_2+2.a_1.(1-a_1).\sigma_1.\sigma_2\)
Utilizando as definições de produto notável, isso é equivalente a:
\(\sigma_{P}^2=[a_1.\sigma_2+(1-a_1).\sigma_2]^{2}\)
Logo, como o que nos interessa para a mensuração do risco do portfólio é o desvio-padrão dele, temos: \(\sigma_{P}=a_1.\sigma_2+(1-a_1).\sigma_2\)
O que significa que o risco do portfólio (desvio-padrão) se torna uma combinação linear do risco (desvio-padrão) dos ativos ponderado pelo share.
Caso 2: Ausência de Correlação, \(\rho_{1,2}=0\)
De maneira similar ao caso 1, temos que ao fazer uso da equação da variância do portfólio:
\(\sigma_{P}^2=a_1^2.\sigma^2_2+(1-a_1)^2.\sigma^2_2\)
Em termos de desvio-padrão, temos:
\(\sigma_{P}=[a_1^2.\sigma^2_2+(1-a_1)^2.\sigma^2_2]^{1/2}\)
O resultado agora é que temos um formato não linear da combinação do risco dos dois ativos. Isso será verificado na próxima figura que teremos uma curvatura na equação risco x retorno. Portanto, há ganhos na diversificação.
Caso 3: Correlação Negativa Perfeita, \(\rho_{1,2}=-1\)
Fazendo uso da equação do portfólio, temos para uma correlação de menos um que:
\(\sigma_{P}^2=a_1^2.\sigma^2_1+(1-a_1)^2.\sigma^2_2-2.a_1.(1-a_1).\sigma_1.\sigma_2\)
Novamente, fazendo uso do conhecimento com produto notável:
\(\sigma_{P}^2=[a_1.\sigma_1-(1-a_1).\sigma_2]^2\)
Em termos de desvio-padrão, torna-se:
\(\sigma_{P}=a_1.\sigma_1-(1-a_1).\sigma_2\)
O terceiro caso nos aponta um ponto importante: A partir de dois ativos arriscados, podemos construir um portfólio livre de risco.1 Para isso, veja a construção:
\(a_1.\sigma_1-(1-a_1).\sigma_2=0\)
Como \(\sigma_1\) e \(\sigma_2\) são exógenos ao problema, iremos deixar como endógena a alocação percentual dos ativos no portfólio afim de construí-lo com risco zero.
\(a_1=\sigma_2/(\sigma_1+\sigma_2)\) enquanto que \(a_2=1-a_1=1-\sigma_2/(\sigma_1+\sigma_2)=\sigma_1/(\sigma_1+\sigma_2)\)
Na sequência o que será feito no script é: a) Montar combinações entre \(a_1\) e \(a_2\) de 0 a 1, com intervalos de 0.01. b) Montar possibilidades de correlação no intervalo de \([-1,1]\) com intervalos de \(0.2\). c) Verificar o formato da correlação para as combinações de portfolio possíveis.
### Dados Estatísticos de Dois Ativos
Ret_1 = 0.08
Ret_2 = 0.12
Std_1 = 0.15
Std_2 = 0.25
# Defina aqui o número de intervalos entre a correlação de -1 a 1.
intervalos = 5
Corr_12 = seq(from =-1,to = 1, by = 1/intervalos)
# Share entre os ativos nos Portfólios
W_1 = seq(from = 0, to = 1, by = 0.01)
W_2 = 1 - W_1
# Retorno do Portfólio de 2 Ativos
Ret_C <- matrix(data = NA,
nrow = length(W_1),
ncol = length(Corr_12))
for (i in 1:length(Corr_12)) {
Ret_C[,i] = W_1*Ret_1 + W_2*Ret_2
}
# Cálculo do Desvio Padrão das Carteiras
Std_C <- matrix(data = NA,
nrow = length(W_1),
ncol = length(Corr_12))
for (i in 1:length(Corr_12)) {
Std_C[,i] = ((W_1^2)*(Std_1^2) + (W_2^2)*(Std_2^2) +
2*W_1*W_2*Std_1*Std_2*Corr_12[i])^(0.5)
}
library(unikn)
my_pal <- usecol(pal_signal,n = 11)
matplot(Std_C,Ret_C, type = "l", col = my_pal,
main = "Portfólio - Retorno versus Risco",
xlab = "Risco - Unidades de Desvio Padrão",
ylab = "Retorno %", lwd = 2, xlim = c(-0.035,0.25))
legend("topleft", legend = as.character(seq(from =-1,to = 1, by = 1/intervalos)),
col = my_pal, lwd = 3, horiz = F, cex = 0.8)
abline(v=0, lty = 2, lwd = 2, col = "black")
abline(v=max(Std_C), lwd =2, lty = 2, col = "black")
Por fim, temos que o retorno de uma carteira livre de risco é de:
Cart_Risc_Zero <- (Std_2/(Std_1 + Std_2))*Ret_1 + (Std_1/(Std_1 + Std_2))*Ret_2
Cart_Risc_Zero## [1] 0.095A Análise de Risco e Retorno de um Portfólio com 3 Ativos
O caso de 2 ativos é mais intuitiva a exploração de possibilidades analíticas para os casos extremos de diversificação. No caso de 3 ativos, temos que o retorno da carteira passa a ser:
\(E(R_P)=a_1.E(R_1)+a_2.E(R_2)+a_3.E(R_3)\)
Em português bem claro, o retorno esperado da carteira é a média ponderada dos retornos esperados ponderados pelos seus devidos shares.
Todavia, no que diz respeito a variância da carteira, temos que:
\(\sigma^2_P=a_1^2.\sigma_1^2+a_2^2.\sigma_2^2+a_3^2.\sigma_3^2+2.(a_1.a_2.\sigma_{12}+a_1.a_3.\sigma_{13}+a_2.a_3.\sigma_{23})\) tendo em vista que \(\sigma_{ij}=\rho_{ij}.\sigma_i.\sigma_j\). Portanto, a equação que originalmente é escrita em termos de variância pode ser reescrita em termos de desvio-padrão e correlação.
O que faremos na sequência é utilizar de geração de números aleatórios (com distribuição uniforme) para gerar possíveis shares para a ação 1, 2 e 3. Como a soma dos valores gerados pode ser inferior a 1, temos que normalizar os valores sorteados.
Isso posto, calcularemos o retorno do portfólio e o risco da carteira a partir de dados definidos anteriormente para: a) retorno esperado do ativo; b) desvio-padrão do retorno do ativo; c) correlação entre o retorno dos ativos.
Ao fim, fazemos uso do pacote ´(IntroCompFinR)´ para identificar a chamada fronteira eficiente. Ela representa a melhor combinação de ativos para os quais há dominância no sentido retorno x risco contas as demais alternativas de igual retorno.
library(varbvs)
Rets <- c(0.1,0.15,0.12)
Stds <- c(0.2,0.25,0.18)
Corr_M <- matrix(data = c(1.0,0.3,0.4,
0.3,1.0,0.3,
0.4,0.3,1.0),
nrow = 3,
ncol = 3)
Pesos <- rand(5000,3)
Soma <- rowSums(Pesos)
Pesos_N <- Pesos/Soma
Ret_C <- Pesos_N[,1]*Rets[1] +
Pesos_N[,2]*Rets[2] +
Pesos_N[,3]*Rets[3]
Var_C <- Pesos_N[,1]^2 * Stds[1]^2 +
Pesos_N[,2]^2 * Stds[2]^2 +
Pesos_N[,3]^2 * Stds[3]^2 +
2*(Pesos_N[,1]*Pesos_N[,2]*Corr_M[2]*Stds[1]*Stds[2] +
Pesos_N[,1]*Pesos_N[,3]*Corr_M[3]*Stds[1]*Stds[3] +
Pesos_N[,2]*Pesos_N[,3]*Corr_M[6]*Stds[2]*Stds[3])
Std_C <- Var_C^(0.5)
plot(Std_C,Ret_C, col = "red",
main = "Diagrama Risco Retorno de 3 Ativos",
xlab = "Risco - Desvio Padrão do Portfólio",
ylab = "Retorno do Portfólio %")
abline(v=min(Std_C), lty = 2, lwd = 2)
### Parte 2
Covs <- c(Corr_M[2]*(Stds[1]*Stds[2]),
Corr_M[3]*(Stds[1]*Stds[3]),
Corr_M[6]*(Stds[2]*Stds[3]))
Covs_C <- matrix(data = c(Stds[1]^2, Covs[1], Covs[2],
Covs[1], Stds[2]^2, Covs[3],
Covs[2], Covs[3], Stds[3]^2),
nrow = 3,
ncol = 3)
#install.packages("IntroCompFinR", repos="http://R-Forge.R-project.org")
library(IntroCompFinR)
ef <- efficient.frontier(Rets, Covs_C, nport=2000)
lines(ef$sd,ef$er, lwd = 2, col = "blue")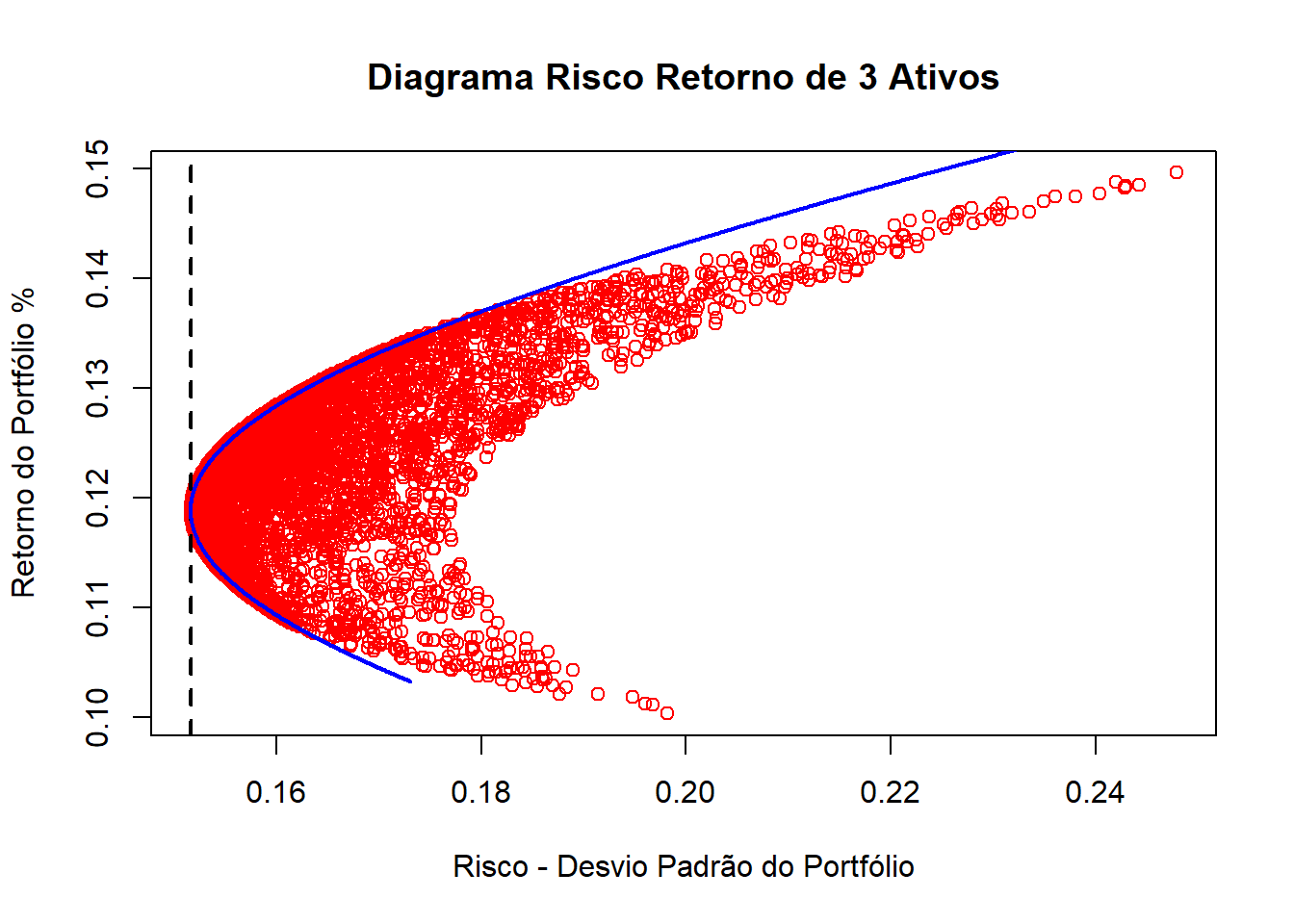
Pelo menos essa possibilidade existe no âmbito teórico. O que na prática impossibilita é que não há dois ativos que tenham o retorno perfeitamente negativo e estável ao longo do tempo.↩