Sidra - Dados do PIB no R

Análise de Conjuntura - Obtenção de Dados do PIB pela SIDRA-IBGE

O economista frequentemente necessita analisar dados sobre o PIB e identificar informações qualitativas sobre a trajetória de uma determinada variável. Nesse sentido, fazemos uso do Markdown para organizar a ideia de obter dados do IBGE, tratá-los para sazonalidade, transformá-los em taxa de crescimento, acumulá-los de um período base igual e identificar a história contada pela trajetória de crescimento acumulado.

Dessa forma, vamos apresentar os pacotes que serão utilizados e a finalidade de cada um deles para o propósito do script.

## Pacotes Utilizados no Script
library(sidrar)
library(seasonal)
library(highcharter)
library(RColorBrewer)
library(widgetframe)

Podemos ver que basicamente utilizaremos 4 pacotes durante o script. O primeiro sidrar é uma library desenvolvida para acessar os dados da plataforma SIDRA-IBGE https://sidra.ibge.gov.br/ via API. O pacote permite o uso de funções como get_sidra() para acessar e realizar o download de uma série desejada de lá.

Para ter conhecimento do código da série desejada, basta pesquisar a série no site e encontrar o link de Parâmetros para a API.

O segundo pacote, seasonal será utilizado para dessazonalizar as séries obtidas através da função seas(). Ela faz uso do protocolo de dessazonalização X-13 ARIMA-SEATS desenvolvido pelo Census Bureau Norte Americano.

O terceiro pacote, highcharter, é um dos mais poderosos pacotes gráficos desenvolvidos para o R (e para outras linguagens também). Ele nos fornece gráficos interativos em HTML, no qual o usuário pode filtrar as séries plotadas, avaliar o valor no ponto do cursor e seu tamanho é ajustado de maneira dinâmica para o tamanho da janela utilizada no navegador.

O quarto pacote, RColorBrewer, nos permite criar gradientes de cores que serão utilizados para colorir a divisão de mandatos presidenciais no gráfico das séries econômicas.

Iremos no primeiro bloco do script capturar os dados e tratá-los para se tornarem séries temporais, ou seja, dados ts. Todavia, inicialmente os dados que chegam estão empilhados. Precisamos então separar em colunas os códigos que os definem por: Agricultura, Indústria, Serviços, PIB, Consumo, Gasto do Governo, Formação Bruta de Capital Fixo, Exportações e Importações. Ao fim, apresentamos as últimas 5 observações da série e plotamos o gráfico para indetificar se há alguma inconsistência nos dados.

## Dados sem ajuste sazonal
tabela = get_sidra(api='/t/1620/n1/all/v/all/p/all/c11255/90687,90691,90696,90707,93404,93405,93406,93407,93408/d/v583%202')

series = c(90687,90691,90696,90707,93404,93405,93406,93407,93408)

names = c('Agro','Ind','Serv','PIB','Consumo','Governo', 'FBCF','Exp','Imp')

pib <- matrix(NA, ncol=length(series),
              nrow=nrow(tabela)/length(series))

for(i in 1:length(series)){
  
  pib[,i] <- tabela$Valor[tabela$`Setores e subsetores (Código)`
                          ==series[i]]
  pib <- ts(pib, start=c(1996,01), freq=4)
  colnames(pib) <- names

}

tail(pib)

##          Agro    Ind   Serv    PIB Consumo Governo   FBCF    Exp    Imp
##  [98,] 269.34 113.29 158.42 151.61  157.88  136.44 128.71 314.10 207.23
##  [99,] 223.06 137.59 171.88 167.19  173.85  140.52 150.53 315.48 208.67
## [100,] 154.15 134.53 179.19 170.10  185.96  146.34 169.80 298.21 248.34
## [101,] 314.40 128.16 172.22 169.04  174.97  136.45 178.79 284.80 266.69
## [102,] 269.49 132.06 175.86 170.26  174.54  144.33 171.29 358.84 249.33
## [103,] 203.08 139.32 181.82 173.88  181.21  145.38 178.76 328.03 251.58

plot(pib, main = "Componentes do PIB", xlab = "Tempo")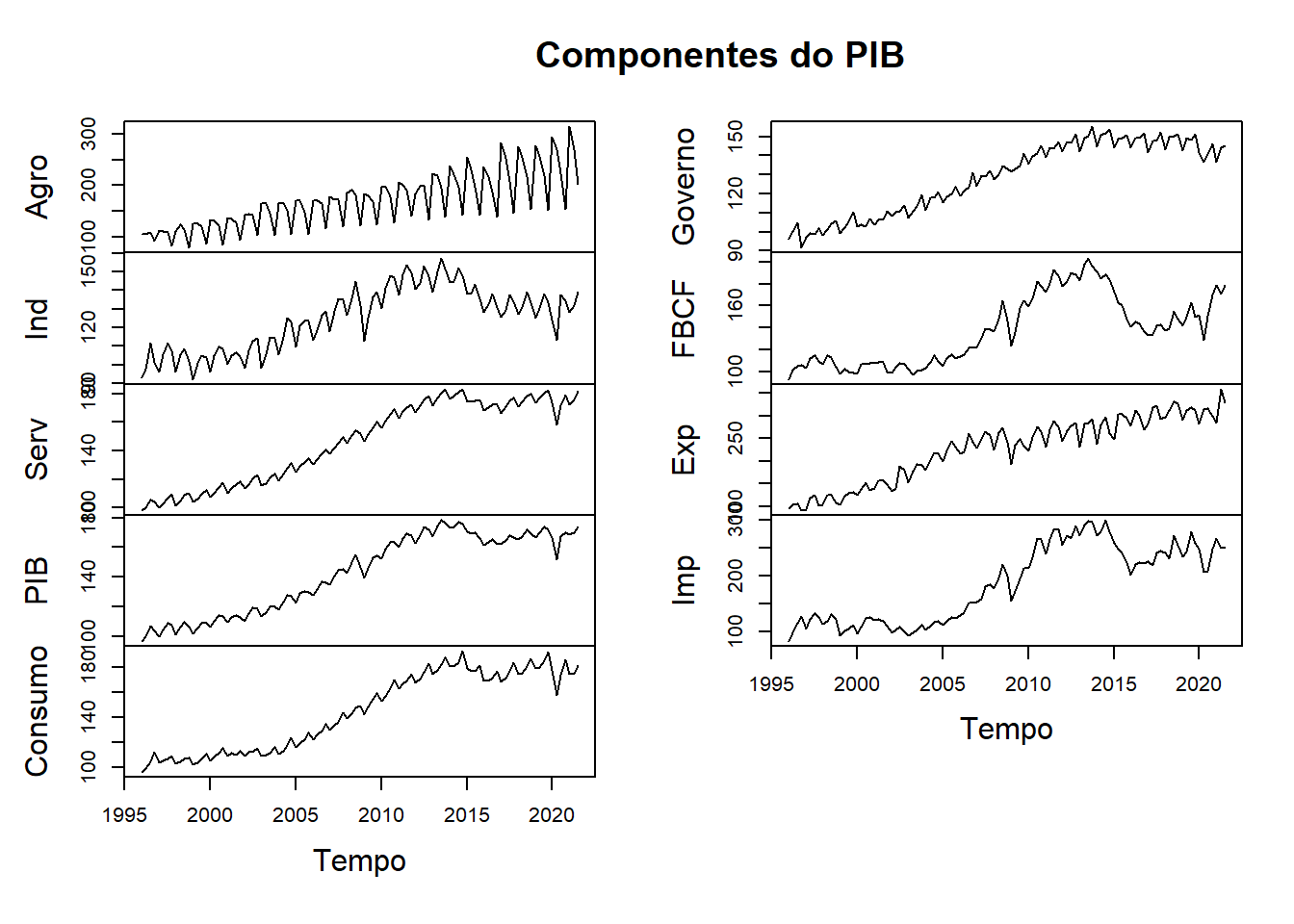

Resumindo, o que estamos verificando são os dados trimestrais (com sazonalidade) da seguinte identidade: \(PIB=Agro+Ind+Ser=C+I+G+X-M\), sendo que \(I=\Delta Estoques+FBCF\). Em outras palavras, estamos lidando com duas óticas distintas para o cálculo do PIB.

Na figura acima foi possível identificar visualmente que a série tem duas características: a) ela está em número índice; b) ela possui carga sazonal;

Em vista disso, iremos tratar a série para sazonalidade e, posteriomente, transformar em taxa de crescimento e acumulá-las a partir de um mesmo ano base. O intuito do segundo exercício é torná-las comparáveis partindo de um ano base escolhido.

Para dessazonalizar, basta usar a função seas() na série desejada.

### Dessazonalização das Rubricas de Oferta
Seas_agr  <- seas(pib[,1])
Seas_ind  <- seas(pib[,2])
Seas_ser  <- seas(pib[,3])

### Dessazonalização do PIB Total
Seas_pib <- seas(pib[,4])

### Dessazonalização das Rubricas de Demanda
Seas_con  <- seas(pib[,5])
Seas_gov  <- seas(pib[,6])
Seas_fbcf <- seas(pib[,7])
Seas_exp  <- seas(pib[,8])
Seas_imp  <- seas(pib[,9])

### Plot comparando o PIB tratado e não tratado (exemplo)
plot(Seas_pib, main = "PIB - Séries: Original e Ajustada",
               ylab = "Valor em Número-Índice",
               xlab = "Tempo", 
               panel.first = grid())
legend("bottomright", c("Ajustada","Original"), 
                      col=c("red", "black"), 
                      lwd = 2, cex=0.8, box.lty=0)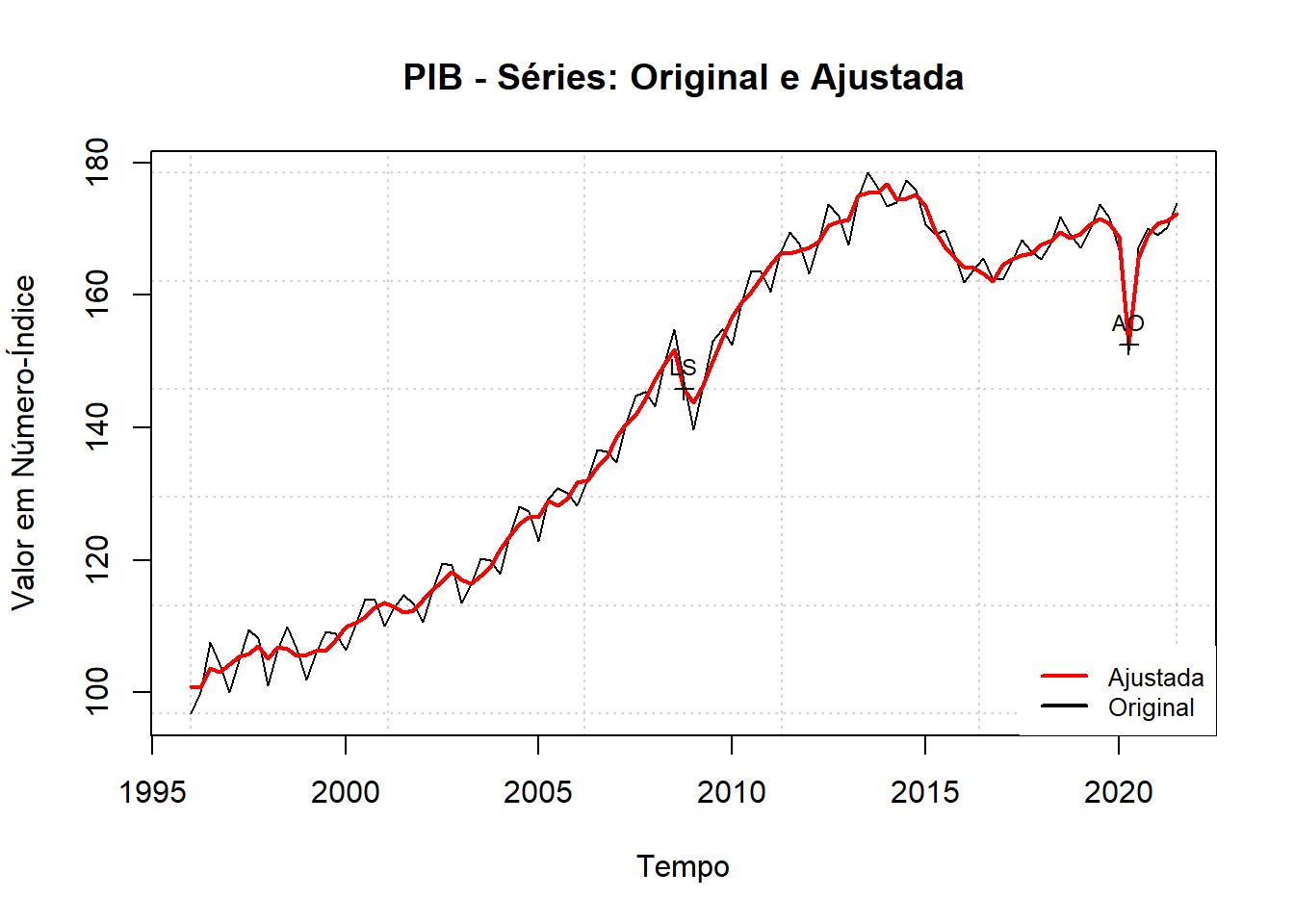

Na parte subsequente do bloco, extraímos a série ajustada (dessazonalizada) e unimos lado a lado cada série temporal tratada. Daí, transformamos em taxa de crescimento a partir de: \(g_y=\Delta Y_t/Y_{t-1}=Y_t/Y_{t-1}-1\), sendo \(g_y\) a taxa de crescimento de uma variável \(Y\) qualquer. Para acumular as taxas a partir de um mesmo ano base, fazemos uso de: \([\prod_{t=1}^T(1+g_y)]-1\). Em termos de linguagem R, aparece através do uso da função cumprod(). Todavia, o seu uso remove a classe ts(). Por essa razão, precisamos declarar novamente como ts()

### Junção dos Componentes do PIB
Agr_Des  <- Seas_agr$data[,3]
Ind_Des  <- Seas_ind$data[,3]
Ser_Des  <- Seas_ser$data[,3]
Pib_Des  <- Seas_pib$data[,3]
Con_Des  <- Seas_con$data[,3]
Gov_Des  <- Seas_gov$data[,3]
FBCF_Des <- Seas_fbcf$data[,3]
Exp_Des  <- Seas_exp$data[,3]
Imp_Des  <- Seas_imp$data[,3]

PIB_D <- cbind(Agr_Des,Ind_Des,Ser_Des,Pib_Des,
               Con_Des,Gov_Des,FBCF_Des,Exp_Des,Imp_Des)

TC_PIB_A  <- (PIB_D/lag(PIB_D,-1)-1)

Agr_ac    <- ts(cumprod(TC_PIB_A[,1]+1)-1, start =c(1996,2), frequency = 4)
Ind_ac    <- ts(cumprod(TC_PIB_A[,2]+1)-1, start =c(1996,2), frequency = 4)
Ser_ac    <- ts(cumprod(TC_PIB_A[,3]+1)-1, start =c(1996,2), frequency = 4)
Pib_ac    <- ts(cumprod(TC_PIB_A[,4]+1)-1, start =c(1996,2), frequency = 4)
Con_ac    <- ts(cumprod(TC_PIB_A[,5]+1)-1, start =c(1996,2), frequency = 4)
Gov_ac    <- ts(cumprod(TC_PIB_A[,6]+1)-1, start =c(1996,2), frequency = 4)
Fbcf_ac   <- ts(cumprod(TC_PIB_A[,7]+1)-1, start =c(1996,2), frequency = 4)
Exp_ac    <- ts(cumprod(TC_PIB_A[,8]+1)-1, start =c(1996,2), frequency = 4)
Imp_ac    <- ts(cumprod(TC_PIB_A[,9]+1)-1, start =c(1996,2), frequency = 4)

No próximo bloco do script, iremos lidar com os belos gráficos do pacote highcharter. Todavia, antes de entrar na plotagem da figura propriamente dita, iremos formatar duas paletas de cores em forma de gradiente. É aqui que iremos fazer uso do pacote RColorBrewer. A primeira paleta de cores é um gradiente que vai dos tons amarelos, passa pelo laranja e termina no vermelho. Pedimos que a sua criação se dê em oito divisões, que coincidem com o número de mandatos políticos. A segunda paleta irá também criar oito intervalos discretos, só que agora com um gradiente indo do amarelo até o verde.

Cores  <- brewer.pal(8, "YlOrRd")
Cores2 <- brewer.pal(8, "YlGn")

Na sequência, fazemos o plot através da função hchart(). Ela nos define a primeira série a ser plotada. As demais entram através do comando hc_add_series. Há um cuidado na escrita. Para que a linha debaixo seja lida como uma continuação do código de plot, devemos no final da linha declarar %>%. A primeira figura plotada é o PIB com a divisão setorial: Serviços, Indústria e Agricultura.

Um outro detalhe a respeito da figura: o comando hc_title() nos permite inserir um título na figura. O comando hc_subtitle() nos permite inserir um rótulo de sub título (abaixo do título). Por fim, o comando hc_xAxis() nos permite rotular o eixo temporal, colocando um nome para um período entre datas, bem como adicionar uma cor de fundo (aqui fazemos uso da paleta criada).

### Figura com o Crescimento Acumulado dos Elementos da Oferta
frameWidget(hchart(Pib_ac, color = "black", name = "PIB - % Acumulado") %>%
  hc_add_series(Agr_ac, color = "blue", name = "Agricultura - % Acumulado") %>%
  hc_add_series(Ind_ac, color = "cyan",  name = "Indústria - % Acumulado") %>%
  hc_add_series(Ser_ac, color = "green",  name = "Serviços - % Acumulado") %>%
  hc_title(text = "Taxa de Crescimento Acumulado dos Componentes da Oferta do PIB", margin = 10,
           style = list(fontSize= "14px")) %>%
  hc_subtitle(text = "Dados Trimestrais: 1T1996 a 2T2019") %>%
  hc_xAxis(plotBands = list(
    list(
      label = list(text = "FHC 1"),
      color = Cores[1],
      from = datetime_to_timestamp(as.Date('1996-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('1998-12-31', tz = 'UTC'))),
    list(
      label = list(text = "FHC 2"),
      color = Cores[2],
      from = datetime_to_timestamp(as.Date('1999-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2002-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Lula 1"),
      color = Cores[3],
      from = datetime_to_timestamp(as.Date('2003-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2006-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Lula 2"),
      color = Cores[4],
      from = datetime_to_timestamp(as.Date('2007-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2010-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Dilma 1"),
      color = Cores[5],
      from = datetime_to_timestamp(as.Date('2011-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2014-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Dilma 2"),
      color = Cores[6],
      from = datetime_to_timestamp(as.Date('2015-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2016-08-31', tz = 'UTC'))),
    list(
      label = list(text = "Temer"),
      color = Cores[7],
      from = datetime_to_timestamp(as.Date('2016-09-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2018-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Bols."),
      color = Cores[8],
      from = datetime_to_timestamp(as.Date('2019-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2020-12-31', tz = 'UTC')))
  )))

Alguns apontamentos qualitativos podem ser feitos sobre a figura acima. O primeiro deles é que a contribuição de cada rubrica fornece ao crescimento agregado é dado por:

\(\Delta Y_t/Y_{t-1}=(Agr_{t-1}/PIB_{t-1})\times \Delta Agro_t/Agro_{t-1}\) \(+(Ind_{t-1}/PIB_{t-1})\times \Delta Ind_t/Ind_{t-1}\) \(+(Ser_{t-1}/PIB_{t-1})\times \Delta Ser_t/Ser_{t-1}\)

Em outras palavras, a contribuição que cada rubrica proporciona ao crescimento agregado é dada pela sua taxa de crescimento vezes o share de participação no produto. Isso posto, temos que a Agricultura tem sido desde 98 o drive de crescimento, crescendo a taxas superiores ao PIB. O setor de serviços cresce bastante colado no ritmo do PIB (o que o leva apenas a manter o share ao longo do tempo). O setor da Indústria (aqui não apenas a de transformação) cresce a taxas mais baixas que o PIB, o que leva a perda de share. Sob o período de crise datado em Dilma 2, temos que todos os setores caem em crescimento acumulado. Todavia, agro volta a recuperar a tendência e a indústria segue em patamares de não recuperação.

Agora, o mesmo exercício que foi feito na figura acima, re-aplicamos para plotar o PIB pela ótica da demanda.

### Figura com o Crescimento Acumulado dos Elementos da Demanda
frameWidget(hchart(Pib_ac, color = "black", name = "PIB - % Acumulado") %>%
  hc_add_series(Con_ac, color = "orange", name = "Consumo - % Acumulado") %>%
  hc_add_series(Gov_ac, color = "purple",  name = "Consumo do Governo - % Acumulado") %>%
  hc_add_series(Fbcf_ac, color = "magenta",  name = "FBCF - % Acumulado") %>%
  hc_add_series(Exp_ac-Imp_ac, color = "red",  name = "Exportações Líquidas - % Acumulado") %>%
    hc_title(text = "Taxa de Crescimento Acumulado dos Componentes da Oferta do PIB", margin = 10,
           style = list(fontSize= "14px")) %>%
  hc_subtitle(text = "Dados Trimestrais: 1T1996 a 2T2019") %>%
  hc_xAxis(plotBands = list(
    list(
      label = list(text = "FHC 1"),
      color = Cores2[1],
      from = datetime_to_timestamp(as.Date('1996-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('1998-12-31', tz = 'UTC'))),
    list(
      label = list(text = "FHC 2"),
      color = Cores2[2],
      from = datetime_to_timestamp(as.Date('1999-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2002-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Lula 1"),
      color = Cores2[3],
      from = datetime_to_timestamp(as.Date('2003-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2006-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Lula 2"),
      color = Cores2[4],
      from = datetime_to_timestamp(as.Date('2007-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2010-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Dilma 1"),
      color = Cores2[5],
      from = datetime_to_timestamp(as.Date('2011-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2014-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Dilma 2"),
      color = Cores2[6],
      from = datetime_to_timestamp(as.Date('2015-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2016-08-31', tz = 'UTC'))),
    list(
      label = list(text = "Temer"),
      color = Cores2[7],
      from = datetime_to_timestamp(as.Date('2016-09-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2018-12-31', tz = 'UTC'))),
    list(
      label = list(text = "Bols."),
      color = Cores2[8],
      from = datetime_to_timestamp(as.Date('2019-01-01', tz = 'UTC')),
      to = datetime_to_timestamp(as.Date('2020-12-31', tz = 'UTC')))
  )))

A respeito do PIB pela ótica da demanda, torna-se notório que há uma queda que antecede a crise. Ela se dá na FBCF (que é privado+público). A inflexão na série começa a partir de 2014. Recentemente, começamos a ter alguma recuperação da mesma Rubrica (todavia em ritmo lendo, o que caracteriza essa crise por ser a de mais lenta recuperação na história da Economia Brasileira Contemporânea).